Exercise 1 Solution (D)
We will use the article. We will use the following article by Flegal et al. (2016).
We will reproduce some results from the article. The authors used NHANES 2013-14 dataset to create their main analytic dataset. The dataset contains 10,175 subjects with 12 relevant variables:
- SEQN: Respondent sequence number
- RIDAGEYR: Age in years at screening
- RIAGENDR: Gender
- DMDEDUC2: Education level
- RIDRETH3: Race/ethnicity
- RIDEXPRG: Pregnancy status at exam
- WTINT2YR: Full sample 2 year weights
- SDMVPSU: Masked variance pseudo-PSU
- SDMVSTRA: Masked variance pseudo-stratum
- BMXBMI: Body mass index in kg/m**2
- SMQ020: Whether smoked at least 100 cigarettes in life
- SMQ040: Current status of smoking (Do you now smoke cigarettes?)
Question 1: Creating data and table
1(a) Importing dataset
1(b) Subsetting according to eligibility
Subset the dataset according to the eligibility criteria described in the second paragraph of the Methods section.
- Hint: The authors restricted their study to
- adults aged 20 years and more,
- non-missing body mass index, and
- non-pregnant.
Your analytic sample size should be 5,455, as described in the first sentence in the Results section.
# 20+
dat.analytic <- subset(dat.full, RIDAGEYR>=20) # N = 5,769
# Non-missing outcome
dat.analytic <- subset(dat.analytic, !is.na(BMXBMI)) # N = 5,520
# Non-pregnant
dat.analytic <- subset(dat.analytic, is.na(RIDEXPRG) | RIDEXPRG !=
"Yes, positive lab pregnancy test") # N = 5,455
dim(dat.analytic)
#> [1] 5455 121(c) Reproduce Table 1
Reproduce Table 1 of the article.
Hint 1: The authors reported unweighted frequencies, and thus, survey features should not be utilized to answer this question. Please be advised to order the categories as shown in the table.
tableonepackage could be helpful.Hint 2: the authors did not show the results for the
Otherrace category. But in your table, you could include all race categories.
library(tableone)
dat <- dat.analytic
# Age
dat$age <- cut(dat$RIDAGEYR, c(20, 40, 60, Inf), right = FALSE)
# Gender
dat$gender <- dat$RIAGENDR
# Race/Hispanic origin group
dat$race <- dat$RIDRETH3
dat$race <- car::recode(dat$race, " 'Non-Hispanic White'='White'; 'Non-Hispanic Black'=
'Black'; 'Non-Hispanic Asian'='Asian'; c('Mexican American',
'Other Hispanic')='Hispanic'; 'Other Race - Including Multi-Rac'=
'Other'; else=NA", levels = c("White", "Black", "Asian",
"Hispanic", "Other"))
# Table 1: Overall
tab11 <- CreateTableOne(vars = "age", strata = "race", data = dat, test = F,
addOverall = T)
# Table 1: Male
tab12 <- CreateTableOne(vars = "age", strata = "race", test = F, addOverall = T,
data = subset(dat, gender == "Male"))
# Table 1: Female
tab13 <- CreateTableOne(vars = "age", strata = "race", test = F, addOverall = T,
data = subset(dat, gender == "Female"))
# Reproducing Table 1
tab1a <- list(Overall = tab11, Male = tab12, Female = tab13)
print(tab1a, format = "f") # Showing only frequencies
#> $Overall
#> Stratified by race
#> Overall White Black Asian Hispanic Other
#> n 5455 2343 1115 623 1214 160
#> age
#> [20,40) 1810 734 362 216 412 86
#> [40,60) 1896 759 383 251 449 54
#> [60,Inf) 1749 850 370 156 353 20
#>
#> $Male
#> Stratified by race
#> Overall White Black Asian Hispanic Other
#> n 2638 1130 556 300 573 79
#> age
#> [20,40) 909 386 182 106 189 46
#> [40,60) 897 360 179 120 215 23
#> [60,Inf) 832 384 195 74 169 10
#>
#> $Female
#> Stratified by race
#> Overall White Black Asian Hispanic Other
#> n 2817 1213 559 323 641 81
#> age
#> [20,40) 901 348 180 110 223 40
#> [40,60) 999 399 204 131 234 31
#> [60,Inf) 917 466 175 82 184 10Question 2
2(a) Reproduce Table 1 with survey features
Not in this article but in many other articles, you would see n comes from the analytic sample and % comes from the survey design that accounts for survey features such as strata, clusters and survey weights. In Question 1, you see how n comes from the analytic sample. Your task for Question 2(a) is to create % part of the Table 1 with survey features, i.e., % should come from the survey design that accounts for strata, clusters and survey weights. You do not need to show the frequiencis but show only the percentages (for categorical variables).
Hints:
Subset the design, not the sample. For this step, you need to work with your full data. If you have generated a variable in your analytic dataset, that variable should also be present in the full dataset.
Generate age, gender, and race variable in your full data. Codes shown in Question 1 could be helpful.
Make the design on the full data and then subset the design.
Reproduce Table 1 with the design from the previous step. The
svyCreateTableOnefunction could be a helpful function.
## Create all variables in the full data
# Age
dat.full$age <- cut(dat.full$RIDAGEYR, c(20, 40, 60, Inf), right = FALSE)
# Gender
dat.full$gender <- dat.full$RIAGENDR
# Race/Hispanic origin group
dat.full$race <- dat.full$RIDRETH3
dat.full$race <- car::recode(dat.full$race, " 'Non-Hispanic White'='White';
'Non-Hispanic Black'='Black'; 'Non-Hispanic Asian'='Asian';
c('Mexican American','Other Hispanic')='Hispanic';
'Other Race - Including Multi-Rac'='Other';
else=NA", levels = c("White", "Black", "Asian",
"Hispanic", "Other"))
# Survey features
dat.full$survey.weight <- dat.full$WTINT2YR
dat.full$psu <- dat.full$SDMVPSU
dat.full$strata <- dat.full$SDMVSTRA
# Subset the design
dat.full$miss <- 1
dat.full$miss[dat.full$SEQN %in% dat.analytic$SEQN] <- 0
svy.design0 <- svydesign(strata = ~strata, id = ~psu, weights = ~survey.weight,
data = dat.full, nest = TRUE)
svy.design <- subset(svy.design0, miss == 0)
# Table 1: Overall
tab11 <- svyCreateTableOne(vars = "age", strata = "race", data = svy.design,
test = F, addOverall = T)
# Table 1: Male
tab12 <- svyCreateTableOne(vars = "age", strata = "race", test = F, addOverall = T,
data = subset(svy.design, gender == "Male"))
# Table 1: Female
tab13 <- svyCreateTableOne(vars = "age", strata = "race", test = F, addOverall = T,
data = subset(svy.design, gender == "Female"))
# Reproducing Table 1
tab1b <- list(Overall = tab11, Male = tab12, Female = tab13)
print(tab1b, format = "p") # Showing only percentages
#> $Overall
#> Stratified by race
#> Overall White Black Asian Hispanic
#> n 217464332.1 143721046.2 24697511.9 11380679.8 31863752.6
#> age (%)
#> [20,40) 35.5 30.8 38.9 40.2 49.6
#> [40,60) 37.5 37.5 39.3 38.5 35.6
#> [60,Inf) 27.0 31.7 21.8 21.2 14.8
#> Stratified by race
#> Other
#> n 5801341.5
#> age (%)
#> [20,40) 49.2
#> [40,60) 38.4
#> [60,Inf) 12.4
#>
#> $Male
#> Stratified by race
#> Overall White Black Asian Hispanic Other
#> n 105744090.8 70126957.2 11285409.5 5233819.5 15947523.0 3150381.6
#> age (%)
#> [20,40) 37.2 32.3 41.3 41.7 51.6 52.9
#> [40,60) 37.6 37.9 39.0 38.5 35.1 36.1
#> [60,Inf) 25.1 29.8 19.7 19.8 13.2 11.0
#>
#> $Female
#> Stratified by race
#> Overall White Black Asian Hispanic Other
#> n 111720241.3 73594089.0 13412102.4 6146860.3 15916229.6 2650960.0
#> age (%)
#> [20,40) 33.8 29.4 36.9 39.0 47.6 44.7
#> [40,60) 37.4 37.1 39.5 38.6 36.0 41.2
#> [60,Inf) 28.8 33.5 23.6 22.5 16.4 14.12(b) Reproduce Table 3
Reproduce the first column of Table 3 of the article (i.e., among men, explore the relationship between obesity and four predictors shown in the table).
If necessary, re-level or re-order the levels.
You need to generate obesity as BMI \(\ge 30 \text{ kg/m}^2\)
You need to generate
smoking statusandeducation. The unweighted frequencies should be matched with the frequencies in eTable 1 and eTable 2. Make sure these variables are in your full dataset as well.Subset the design, not the sample.
Fit the model. Do not need to report the model summary.
The authors used SAS to produce the results vs. We are using R. The estimates could be slightly different (in second decimal point) from the estimates presented in Table 3, but they should be approximately similar.
You can use
Publishorjtoolspackage to report the odds ratios. Your odds ratios could be look like as follows:
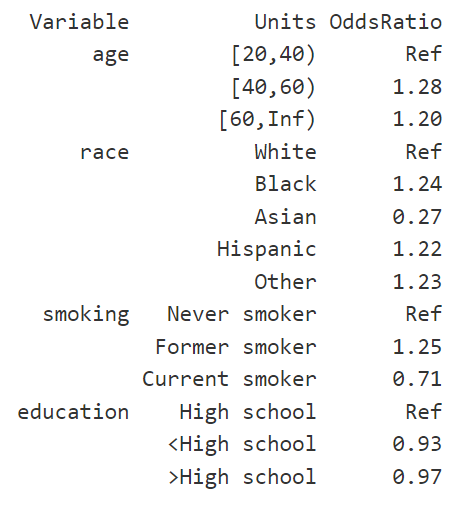
# Obese
dat.full$obese <- ifelse(dat.full$BMXBMI >= 30, "Yes", "No")
# Smoking status
dat.full$smoking <- dat.full$SMQ020
dat.full$smoking <- car::recode(dat.full$smoking, " 'Yes'='Current smoker';
'No'='Never smoker'; else=NA",
levels = c("Never smoker", "Former smoker",
"Current smoker"))
dat.full$smoking[dat.full$SMQ040 == "Not at all"] <- "Former smoker"
# Education
dat.full$education <- dat.full$DMDEDUC2
dat.full$education <- car::recode(dat.full$education, " c('Some college or AA degree',
'College graduate or above') = '>High school';
'High school graduate/GED or equi' = 'High school';
c('Less than 9th grade',
'9-11th grade (Includes 12th grad') = '<High school';
else = NA", levels = c("High school", "<High school",
">High school"))
# Survey features
dat.full$survey.weight <- dat.full$WTINT2YR
dat.full$psu <- dat.full$SDMVPSU
dat.full$strata <- dat.full$SDMVSTRA
# Subset the design
dat.full$miss <- 1
dat.full$miss[dat.full$SEQN %in% dat.analytic$SEQN] <- 0
svy.design0 <- svydesign(strata = ~strata, id = ~psu, weights = ~survey.weight,
data = dat.full, nest = TRUE)
svy.design <- subset(svy.design0, miss == 0)
# Table 3 - column 1
fit.male <- svyglm(I(obese=="Yes") ~ age + race + smoking + education,
family = binomial, design = subset(svy.design, gender == "Male"))
#> Warning in eval(family$initialize): non-integer #successes in a binomial glm!
publish(fit.male)
#> Variable Units OddsRatio CI.95 p-value
#> age [20,40) Ref
#> [40,60) 1.28 [0.94;1.74] 0.173590
#> [60,Inf) 1.20 [0.77;1.85] 0.458803
#> race White Ref
#> Black 1.24 [0.93;1.65] 0.202249
#> Asian 0.27 [0.20;0.37] 0.000345
#> Hispanic 1.22 [0.88;1.69] 0.293132
#> Other 1.23 [0.67;2.23] 0.532168
#> smoking Never smoker Ref
#> Former smoker 1.25 [0.96;1.64] 0.157176
#> Current smoker 0.71 [0.55;0.92] 0.047198
#> education High school Ref
#> <High school 0.93 [0.67;1.29] 0.685577
#> >High school 0.97 [0.72;1.29] 0.8213572(c) Model selection
From the literature, you know that age and race needs to be adjusted in the model, but you are not sure about smoking and education. Run an AIC based backward selection process to figure out whether you want to add smoking or education, or both in the final model in 2(b). What is your conclusion, i.e., which variables are selected/dropped [Expected answer: one short sentence]?
Hints:
Your design must be free from missing values. Even after applying eligibility criteria, you may have some missing values on multiple variables (see eTable 1 and eTable 2). This is especially important for model selection process.
You can create a complete case analytic dataset (i.e., dataset without missing values in obesity, four predictors, and survey features). Then create the design on the full data and subset the design for the complete case samples.
stepfunction could be helpful.
# Obese
dat$obese <- ifelse(dat$BMXBMI >= 30, "Yes", "No")
dat$obese <- factor(dat$obese, levels = c("No", "Yes"))
# Smoking status
dat$smoking <- dat$SMQ020
dat$smoking <- car::recode(dat$smoking, " 'Yes'='Current smoker';
'No'='Never smoker'; else=NA",
levels = c("Never smoker", "Former smoker",
"Current smoker"))
dat$smoking[dat$SMQ040 == "Not at all"] <- "Former smoker"
# Education
dat$education <- dat$DMDEDUC2
dat$education <- car::recode(dat$education, " c('Some college or AA degree',
'College graduate or above') = '>High school';
'High school graduate/GED or equi' = 'High school';
c('Less than 9th grade',
'9-11th grade (Includes 12th grad') = '<High school';
else = NA", levels = c("High school", "<High school",
">High school"))
# Survey design
dat$survey.weight <- dat$WTINT2YR
dat$psu <- dat$SDMVPSU
dat$strata <- dat$SDMVSTRA
# Select only relevant variables
dat2 <- dat[,c("SEQN", "age", "race", "smoking", "education",
"survey.weight", "psu", "strata")]
# Remove missing values
dat2 <- dat2[complete.cases(dat2),] # 5 missing values dropped
# Subset the design
dat.full$miss <- 1
dat.full$miss[dat.full$SEQN %in% dat2$SEQN] <- 0
svy.design0 <- svydesign(strata = ~strata, id = ~psu, weights = ~survey.weight,
data = dat.full, nest = TRUE)
svy.design <- subset(svy.design0, miss == 0)
# Initial model
fit1 <- svyglm(I(obese=="Yes") ~ age + race + smoking + education,
family = binomial, design = subset(svy.design, gender == "Male"))
#> Warning in eval(family$initialize): non-integer #successes in a binomial glm!
scope <- list(upper = ~ age + race + smoking + education,
lower = ~ age + race)
# Final model: Backward elimination using the AIC criteria
fit2 <- step(fit1, scope = scope, trace = FALSE, k = 2, direction = "backward")
#> Warning in eval(family$initialize): non-integer #successes in a binomial glm!
#> Warning in eval(family$initialize): non-integer #successes in a binomial glm!
#> Warning in eval(family$initialize): non-integer #successes in a binomial glm!
#> Warning in eval(family$initialize): non-integer #successes in a binomial glm!
#> Warning in eval(family$initialize): non-integer #successes in a binomial glm!
#> Warning in eval(family$initialize): non-integer #successes in a binomial glm!
#> Warning in eval(family$initialize): non-integer #successes in a binomial glm!
#> Warning in eval(family$initialize): non-integer #successes in a binomial glm!
# Summary of the final model
publish(fit2)
#> Variable Units OddsRatio CI.95 p-value
#> age [20,40) Ref
#> [40,60) 1.28 [0.94;1.73] 0.15579
#> [60,Inf) 1.19 [0.76;1.86] 0.46397
#> race White Ref
#> Black 1.23 [0.92;1.65] 0.19682
#> Asian 0.27 [0.20;0.37] < 1e-04
#> Hispanic 1.21 [0.90;1.61] 0.24507
#> Other 1.23 [0.68;2.23] 0.52048
#> smoking Never smoker Ref
#> Former smoker 1.25 [0.96;1.64] 0.14296
#> Current smoker 0.71 [0.54;0.92] 0.03895The education variable is dropped from the final model.
2(d) Testing for interactions
Check whether the interaction between age and smoking should be added in the 2(b) model (yes or no answer required, along with the code and p-value):
No. We won’t keep the age and smoking interaction.