PSM in OA-CVD (CCHS)
This tutorial is a comprehensive guide on implementing Propensity Score Matching (PSM) using R, particularly focusing on a OA - CVD health study from the Canadian Community Health Survey (CCHS). This PSM method is used to reduce bias due to confounding variables in observational studies by matching treated and control units with similar propensity scores. The tutorial illustrates that PSM is an iterative process, where researchers may need to refine their matching strategy to achieve satisfactory balance in the matched sample. Different strategies for estimating the treatment effect in the matched sample are explored, each with its own assumptions and implications.
Load packages
At first, various R packages are loaded to utilize their functions for data manipulation, statistical analysis, and visualization.
Load data
The dataset is loaded into the R environment. Variables are renamed to avoid conflicts in subsequent analyses.
Analysis
We are going to apply propensity score analysis (Matching) in our OA - CVD problem from CCHS. For computation considerations, we will only work with cycle 1.1, and the people from Northern provinces in Canada (analytic11n data).
Step 1
Specify PS
A logistic regression model formula is specified to calculate the propensity scores (PS), which is the probability of receiving the treatment given the observed covariates.
ps.formula <- as.formula("OA ~ age + sex + stress + married +
income + race + bmi + phyact + smoke +
doctor + drink + bp +
immigrate + fruit + diab + edu")
var.names <- c("age", "sex", "stress", "married",
"income", "race", "bmi", "phyact", "smoke",
"doctor", "drink", "bp",
"immigrate", "fruit", "diab", "edu")Fit model
The software fits the PS model using a logistic regression by default. This package actually performs step 1 and 2 with one command matchit.
Look at the website for arguments of matchit (RDocumentation 2023)]. It looks like this
Nearest-Neighbor Matching:
Nearest-neighbor matching is a widely used technique in PSM to pair treated and control units based on the proximity of their propensity scores. It is straightforward and computationally efficient, making it a popular choice in many applications of PSM. Nearest-neighbor matching is often termed a “greedy” algorithm because it matches units in order, without considering the global distribution of propensity scores. Once a match is made, it is not revisited, even if a later unit would have been a better match. The method seeks to minimize bias by creating closely matched pairs but can increase variance if the pool of potential matches is reduced too much (e.g., using a very narrow caliper). It is essential to ensure that there is a common support region where the distributions of propensity scores for treated and control units overlap, ensuring comparability.
Step 2
Match subjects by PS
We are going to match using a Nearest neighbor algorithm. This is a greedy matching algorithm. Note that we are not even defining any caliper.
Caliper:
In the context of PSM, a caliper is a predefined maximum allowable difference between the propensity scores of matched units. Essentially, it sets a threshold for how dissimilar matched units can be in terms of their propensity scores. When a caliper is used, a treated unit is only matched with a control unit if the absolute difference in their propensity scores is less than or equal to the specified caliper width. The caliper is used to avoid bad matches and thereby minimize bias in the estimated treatment effect. The size of the caliper is crucial. Too wide a caliper may allow poor matches, while too narrow a caliper may result in many units going unmatched. Implementing a caliper involves a trade-off between bias and efficiency. Using a caliper reduces bias by avoiding poor matches but may increase variance by reducing the number of matched pairs available for analysis. Therefore, the use of a caliper in PSM is a strategic decision to enhance the quality of matches and thereby improve the validity of causal inferences drawn from observational data. It is a practical tool to ensure that matched units are sufficiently similar in terms of their propensity scores, reducing the likelihood of bias due to poor matches.
# set seed
set.seed(123)
# match
matching.obj <- matchit(ps.formula,
data = analytic11n,
method = "nearest",
ratio = 1)
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
# see how many matched
matching.obj
#> A `matchit` object
#> - method: 1:1 nearest neighbor matching without replacement
#> - distance: Propensity score
#> - estimated with logistic regression
#> - number of obs.: 1424 (original), 134 (matched)
#> - target estimand: ATT
#> - covariates: age, sex, stress, married, income, race, bmi, phyact, smoke, doctor, drink, bp, immigrate, fruit, diab, edu
# create the "matched"" data
OACVD.match <- match.data(matching.obj)
# see the dimension
dim(analytic11n)
#> [1] 1424 23
dim(OACVD.match)
#> [1] 134 26Let’s try to understand how this is working.
Extract matched IDs
Extract the matched treated IDs
treated.id<-as.numeric(row.names(m.mat))
treated.id # basically row names
#> [1] 17864 17921 18191 18256 18264 18383 18389 18475 39105 96344
#> [11] 96364 96407 96424 96460 96484 96571 96582 96625 96632 96641
#> [21] 96657 96686 96693 96696 96705 96734 96795 96840 96913 97027
#> [31] 97065 97125 108178 108183 108185 108192 111809 111813 111856 111859
#> [41] 111895 111896 111920 111942 112014 112026 112046 112083 112086 112114
#> [51] 112122 112151 112167 112189 112197 112215 112232 112245 112275 112284
#> [61] 112289 112290 112300 112325 112375 126477 126522Extract the matched untreated IDs
untreated.id <- as.numeric(m.mat)
untreated.id # basically row names
#> [1] 96719 17846 97168 111999 17989 108197 112384 17909 126561 111880
#> [11] 112184 18117 96865 18120 97023 112379 97017 126562 96356 126470
#> [21] 126385 96374 18203 18262 96972 111924 96354 96983 18235 96882
#> [31] 112054 18321 112349 18426 38996 126516 111814 112087 96569 111932
#> [41] 126539 18315 96665 18225 112052 112324 112165 18329 96609 126376
#> [51] 96474 126570 126547 126343 96680 96558 111931 96718 96533 111823
#> [61] 112177 17953 17904 111908 111962 96644 96576Extract the matched treated data
Extract the matched untreated data
Extract the matched data altogether
Simply using match.data is enough (as done earlier).
Assign match ID
OACVD.match$match.ID <- NA
OACVD.match$match.ID[rownames(OACVD.match) %in% treated.id] <- 1:length(treated.id)
OACVD.match$match.ID[rownames(OACVD.match) %in% untreated.id] <- 1:length(untreated.id)
table(OACVD.match$match.ID)
#>
#> 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
#> 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
#> 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#> 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67
#> 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2Take a look at individual matches for the first match
Take a look at individual matches for the second match
Step 3
Both graphical and numerical methods are used to assess the quality of the matches and the balance of covariates in the matched sample.
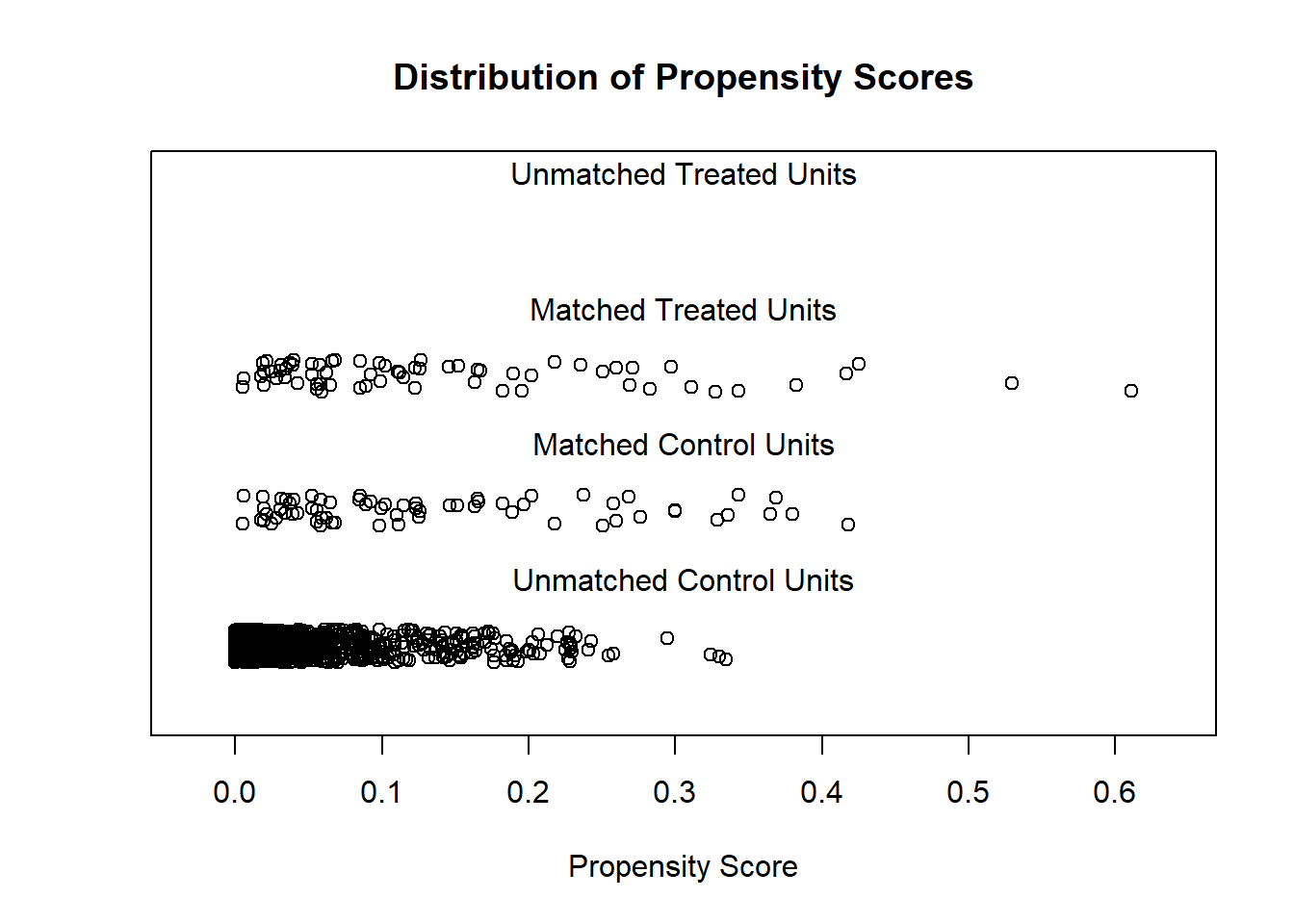
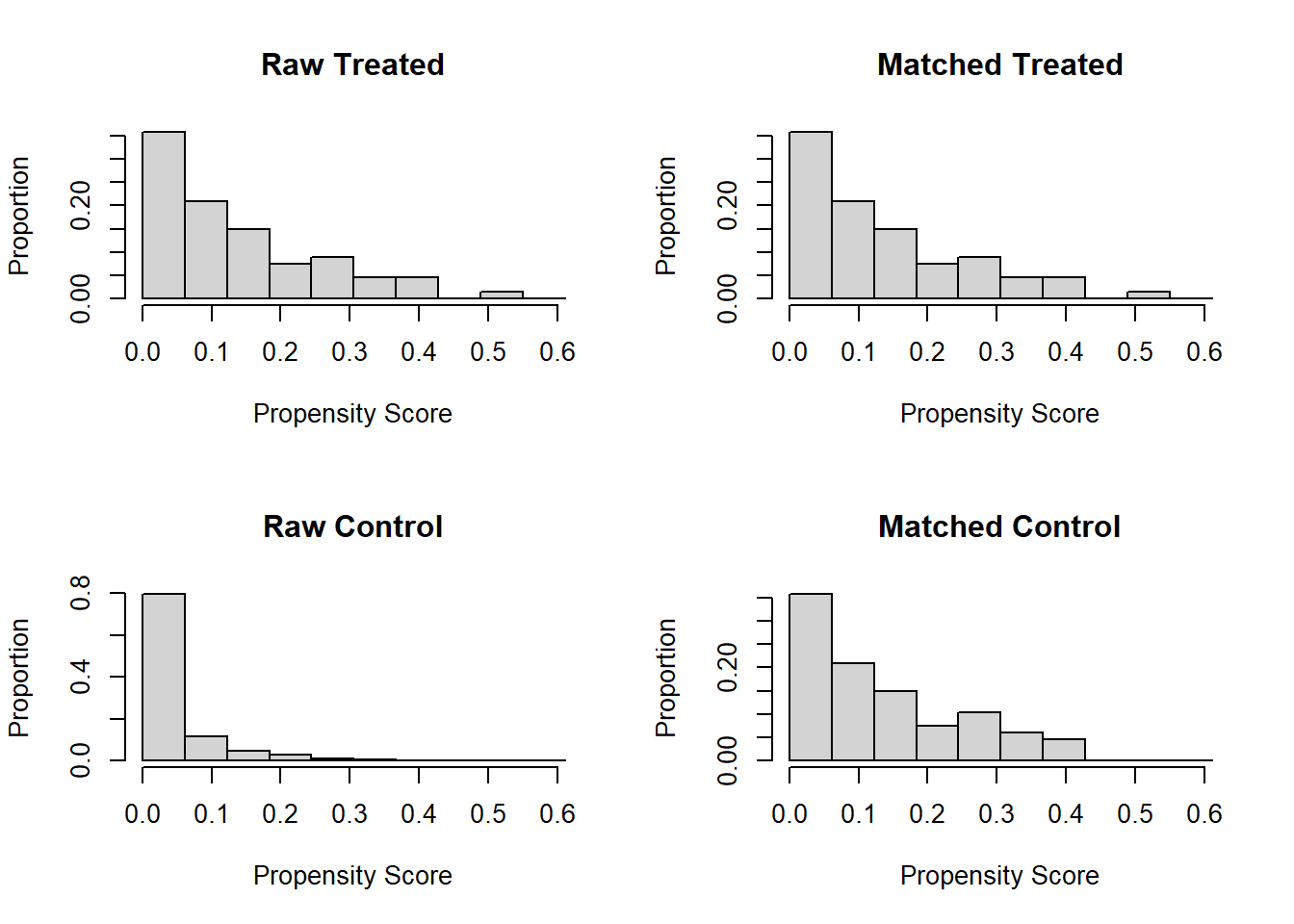
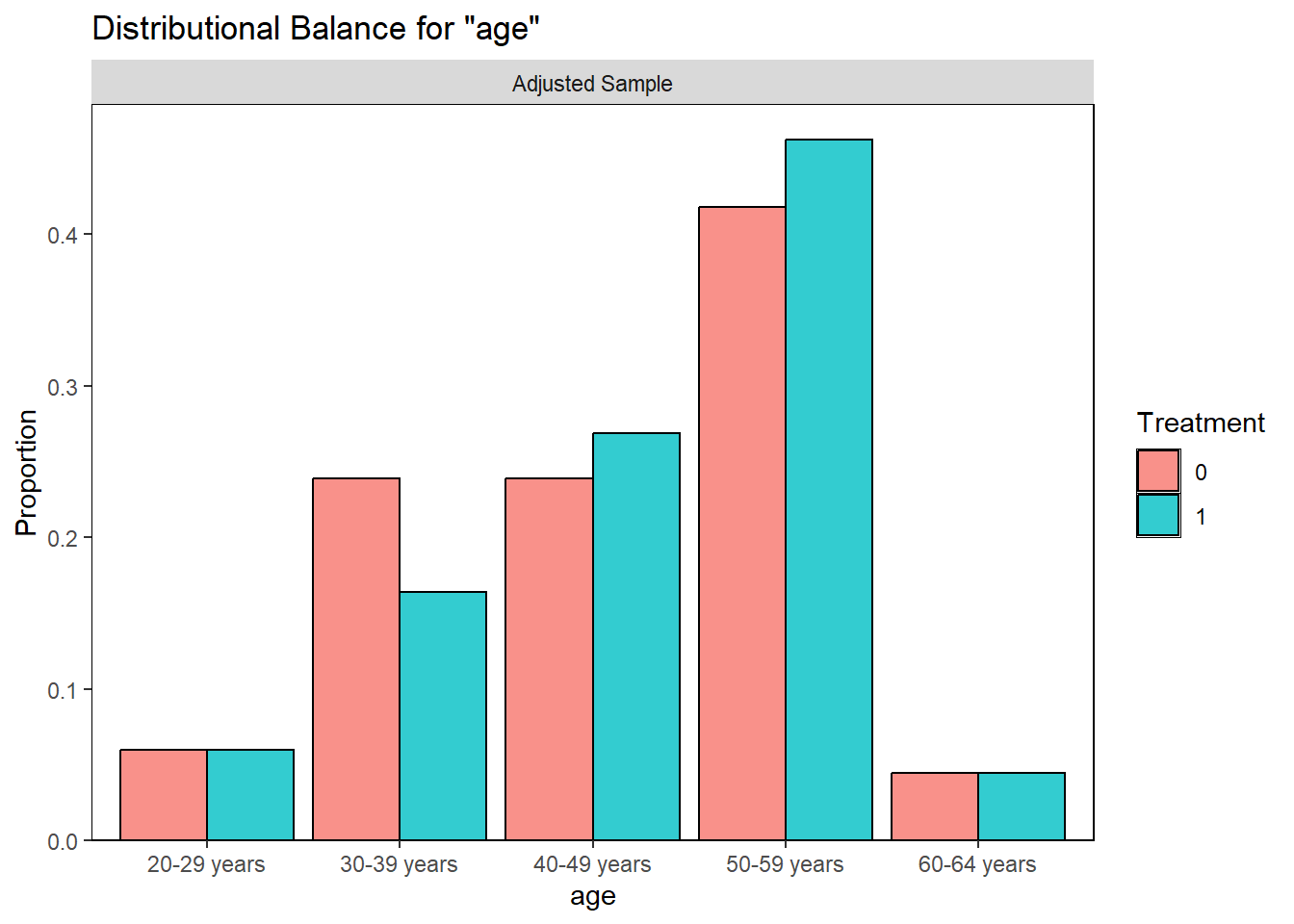
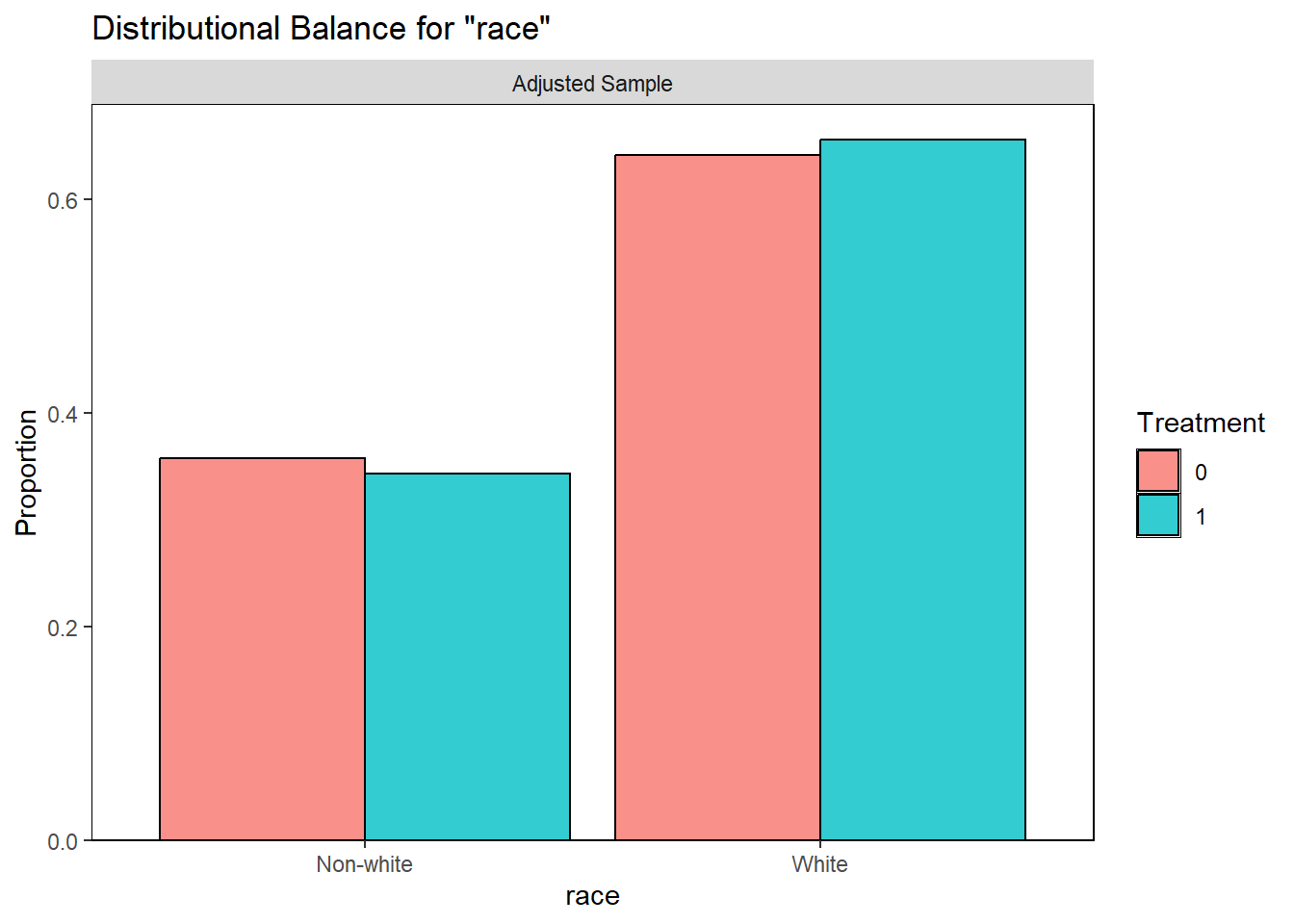
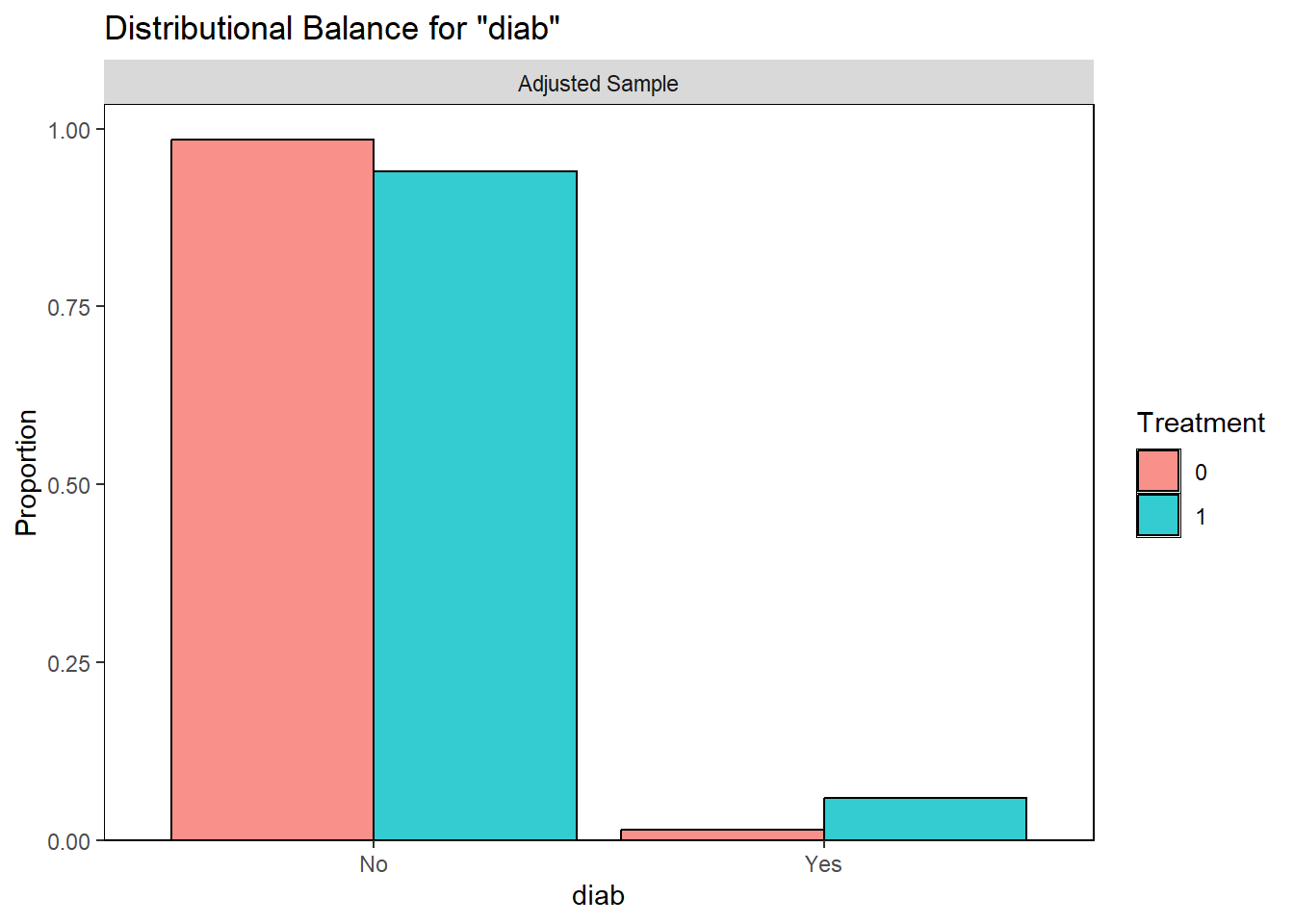
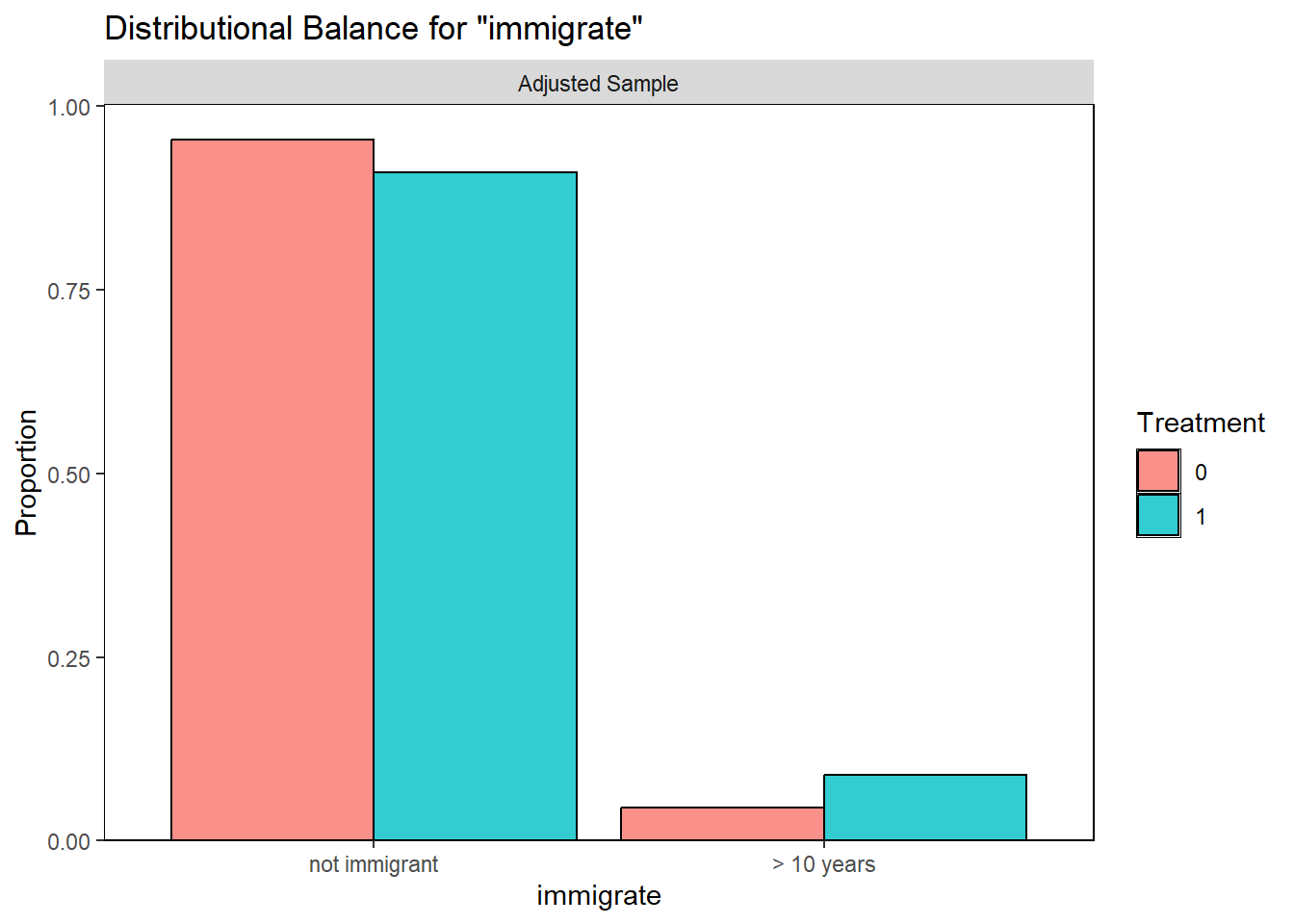
Examining PS graphically
Visually inspect the PS and assess the balance of covariates in the matched sample. Various plots are generated to visualize the distribution of PS across treatment groups and to check the balance of covariates before and after matching.
matchit package
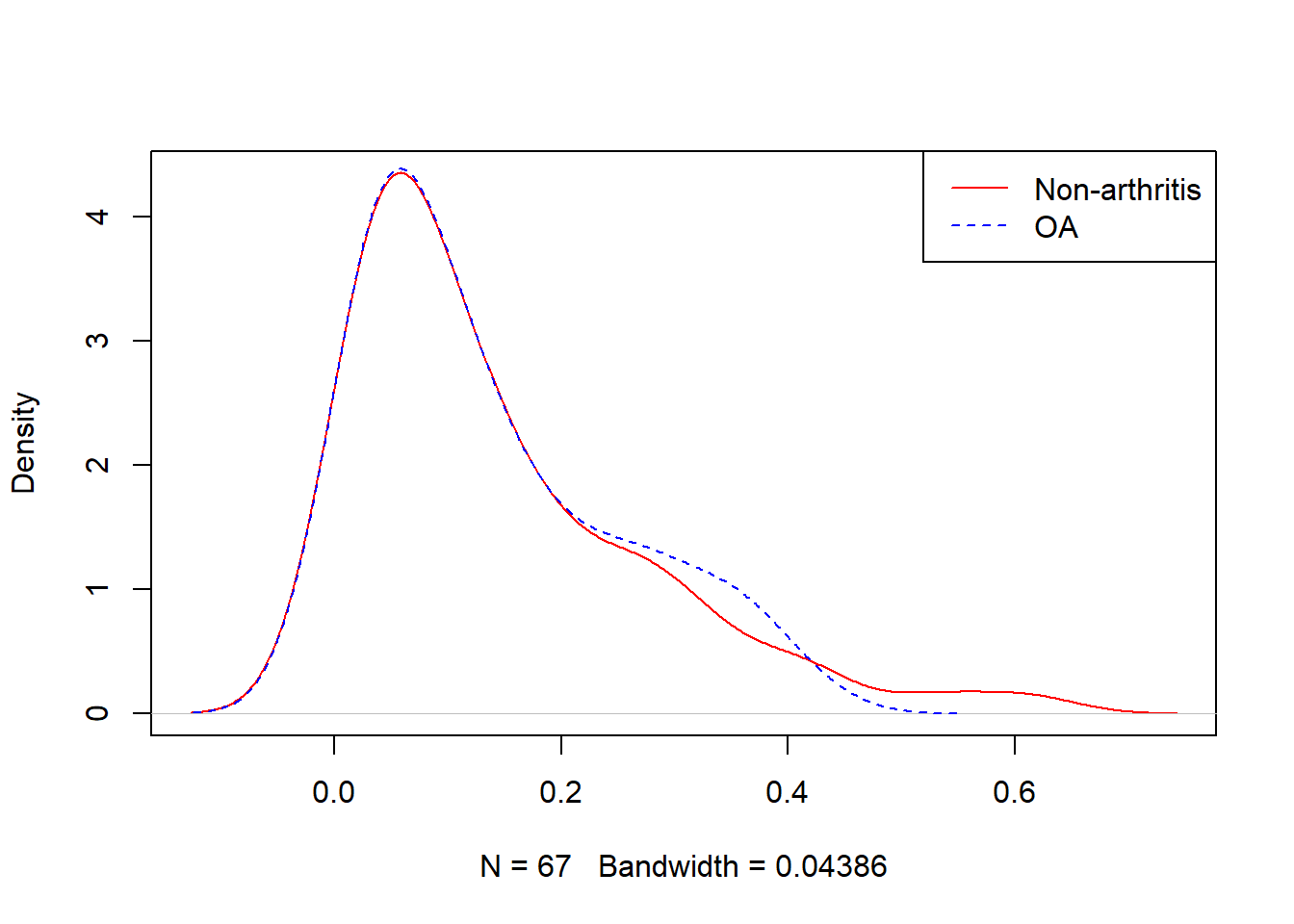
Overalp check
cobalt package
Overlap check in a more convenient way
Look at the data
Numerical values of PS
summary(OACVD.match$distance)
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.004671 0.044834 0.099094 0.138969 0.200576 0.611166
by(OACVD.match$distance, OACVD.match$OA, summary)
#> OACVD.match$OA: 0
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.004671 0.047344 0.099215 0.135042 0.199279 0.418206
#> ------------------------------------------------------------
#> OACVD.match$OA: 1
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.004671 0.047346 0.098973 0.142897 0.198741 0.611166Question for the students
- Are you happy with the matching after reviewing the plots?
Covariate balance in matched sample
Covariate balance is assessed numerically using standardized mean differences (SMD).
Standardized mean differences: SMD is a versatile and widely used statistical measure that facilitates the comparison of groups in research by providing a scale-free metric of difference and balance. In the context of propensity score matching, achieving low SMD values for covariates after matching is crucial to ensuring the validity of causal inferences drawn from the matched sample.
Benifits:
- SMD is not influenced by the scale of the measured variable, making it suitable for comparing the balance of different variables measured on different scales.
- Unlike hypothesis testing, SMD is not affected by sample size, making it a reliable measure for assessing balance in matched samples.
tab1 <- CreateTableOne(strata = "OA", data = OACVD.match,
test = FALSE, vars = var.names)
print(tab1, smd = TRUE)
#> Stratified by OA
#> 0 1 SMD
#> n 67 67
#> age (%) 0.190
#> 20-29 years 4 ( 6.0) 4 ( 6.0)
#> 30-39 years 16 (23.9) 11 (16.4)
#> 40-49 years 16 (23.9) 18 (26.9)
#> 50-59 years 28 (41.8) 31 (46.3)
#> 60-64 years 3 ( 4.5) 3 ( 4.5)
#> 65 years and over 0 ( 0.0) 0 ( 0.0)
#> teen 0 ( 0.0) 0 ( 0.0)
#> sex = Male (%) 28 (41.8) 32 (47.8) 0.120
#> stress = stressed (%) 20 (29.9) 21 (31.3) 0.032
#> married = single (%) 22 (32.8) 23 (34.3) 0.032
#> income (%) 0.183
#> $29,999 or less 11 (16.4) 13 (19.4)
#> $30,000-$49,999 19 (28.4) 15 (22.4)
#> $50,000-$79,999 14 (20.9) 12 (17.9)
#> $80,000 or more 23 (34.3) 27 (40.3)
#> race = White (%) 43 (64.2) 44 (65.7) 0.031
#> bmi (%) <0.001
#> Underweight 0 ( 0.0) 0 ( 0.0)
#> healthy weight 18 (26.9) 18 (26.9)
#> Overweight 49 (73.1) 49 (73.1)
#> phyact (%) 0.041
#> Active 16 (23.9) 16 (23.9)
#> Inactive 40 (59.7) 39 (58.2)
#> Moderate 11 (16.4) 12 (17.9)
#> smoke (%) 0.258
#> Never smoker 14 (20.9) 9 (13.4)
#> Current smoker 20 (29.9) 27 (40.3)
#> Former smoker 33 (49.3) 31 (46.3)
#> doctor = Yes (%) 51 (76.1) 47 (70.1) 0.135
#> drink (%) 0.116
#> Never drank 2 ( 3.0) 2 ( 3.0)
#> Current drinker 54 (80.6) 51 (76.1)
#> Former driker 11 (16.4) 14 (20.9)
#> bp = Yes (%) 7 (10.4) 5 ( 7.5) 0.105
#> immigrate (%) 0.180
#> not immigrant 64 (95.5) 61 (91.0)
#> > 10 years 3 ( 4.5) 6 ( 9.0)
#> recent 0 ( 0.0) 0 ( 0.0)
#> fruit (%) 0.146
#> 0-3 daily serving 19 (28.4) 19 (28.4)
#> 4-6 daily serving 28 (41.8) 32 (47.8)
#> 6+ daily serving 20 (29.9) 16 (23.9)
#> diab = Yes (%) 1 ( 1.5) 4 ( 6.0) 0.238
#> edu (%) 0.105
#> < 2ndary 14 (20.9) 13 (19.4)
#> 2nd grad. 1 ( 1.5) 2 ( 3.0)
#> Other 2nd grad. 1 ( 1.5) 1 ( 1.5)
#> Post-2nd grad. 51 (76.1) 51 (76.1)Question for the students
- All SMD < 0.20?
Other balance measures
Individual categories
If you want to check balance at each category (not very useful in general situations). We are generally interested if the variables are balanced or not (not categories).
baltab <- bal.tab(matching.obj)
baltab
#> Balance Measures
#> Type Diff.Adj
#> distance Distance 0.0597
#> age_20-29 years Binary 0.0000
#> age_30-39 years Binary -0.0746
#> age_40-49 years Binary 0.0299
#> age_50-59 years Binary 0.0448
#> age_60-64 years Binary 0.0000
#> sex_Male Binary 0.0597
#> stress_stressed Binary 0.0149
#> married_single Binary 0.0149
#> income_$29,999 or less Binary 0.0299
#> income_$30,000-$49,999 Binary -0.0597
#> income_$50,000-$79,999 Binary -0.0299
#> income_$80,000 or more Binary 0.0597
#> race_White Binary 0.0149
#> bmi_Underweight Binary 0.0000
#> bmi_healthy weight Binary 0.0000
#> bmi_Overweight Binary 0.0000
#> phyact_Active Binary 0.0000
#> phyact_Inactive Binary -0.0149
#> phyact_Moderate Binary 0.0149
#> smoke_Never smoker Binary -0.0746
#> smoke_Current smoker Binary 0.1045
#> smoke_Former smoker Binary -0.0299
#> doctor_Yes Binary -0.0597
#> drink_Never drank Binary 0.0000
#> drink_Current drinker Binary -0.0448
#> drink_Former driker Binary 0.0448
#> bp_Yes Binary -0.0299
#> immigrate_not immigrant Binary -0.0448
#> immigrate_> 10 years Binary 0.0448
#> immigrate_recent Binary 0.0000
#> fruit_0-3 daily serving Binary 0.0000
#> fruit_4-6 daily serving Binary 0.0597
#> fruit_6+ daily serving Binary -0.0597
#> diab_Yes Binary 0.0448
#> edu_< 2ndary Binary -0.0149
#> edu_2nd grad. Binary 0.0149
#> edu_Other 2nd grad. Binary 0.0000
#> edu_Post-2nd grad. Binary 0.0000
#>
#> Sample sizes
#> Control Treated
#> All 1357 67
#> Matched 67 67
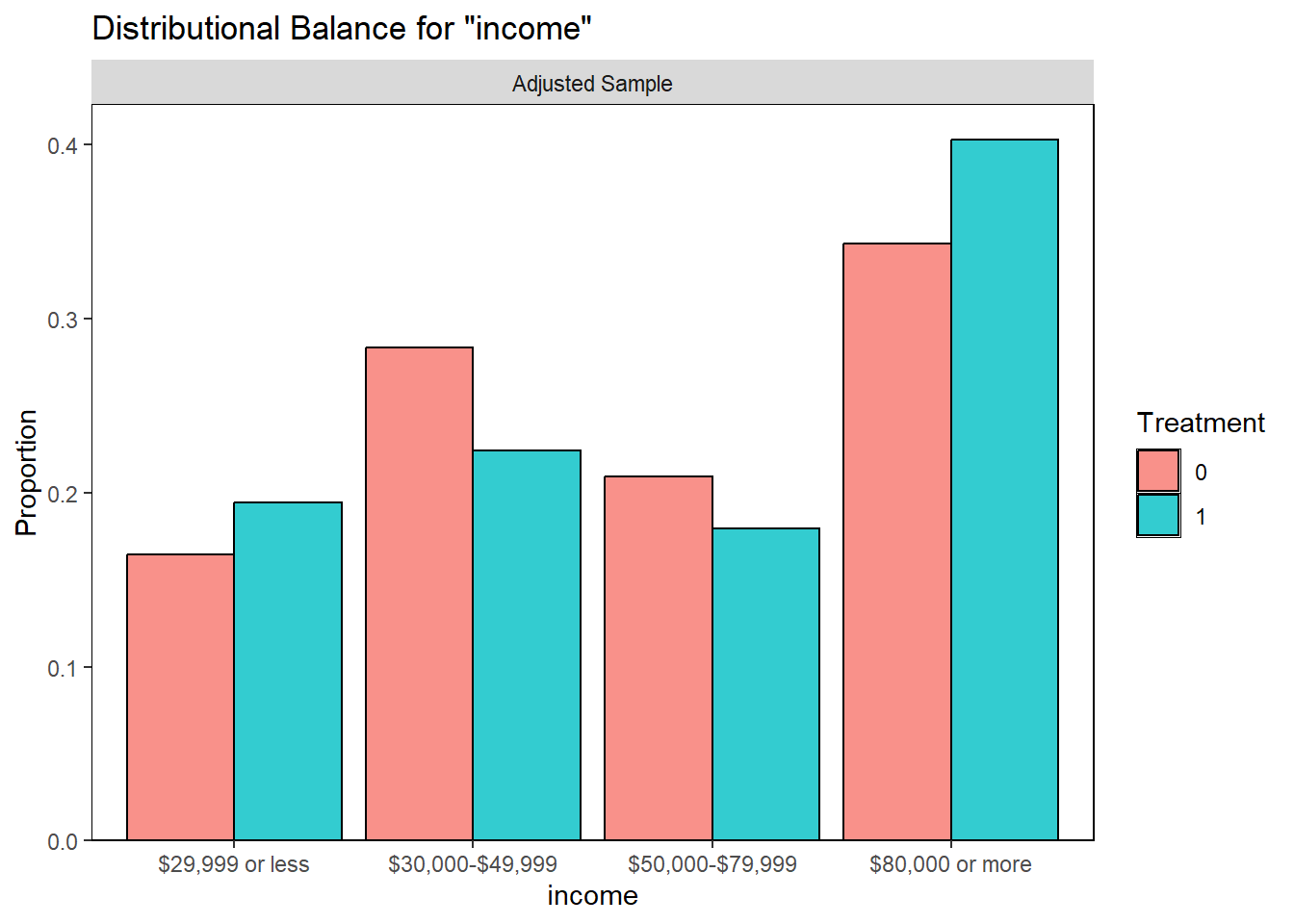
#> Unmatched 1290 0Individual plots
You could plot each variables individually
Love plot
# Individual categories again
love.plot(baltab, threshold = .2)
#> Warning: Unadjusted values are missing. This can occur when `un = FALSE` and
#> `quick = TRUE` in the original call to `bal.tab()`.
#> Warning: Standardized mean differences and raw mean differences are present in
#> the same plot. Use the `stars` argument to distinguish between them and
#> appropriately label the x-axis. See `?love.plot` for details.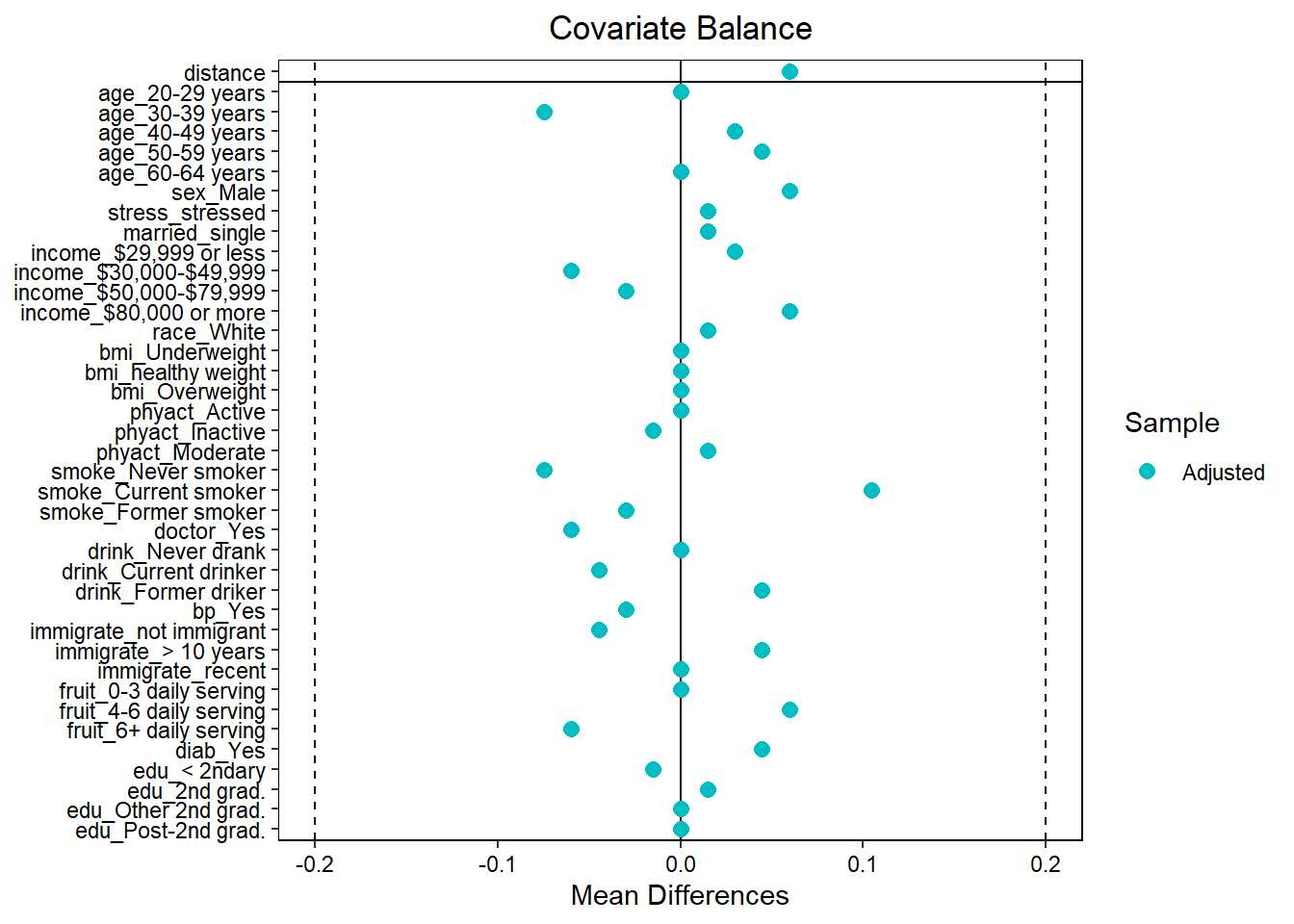
Repeat of Step 1-3 again
Covariate balance is reassessed in each step to ensure the quality of the match.
Add caliper
The matching process is repeated, this time introducing a caliper to ensure that matches are only made within a specified range of PS.
logitPS <- -log(1/OACVD.match$distance - 1)
# logit of the propensity score
.2*sd(logitPS) # suggested in the literature
#> [1] 0.2334615
# Step 1 and 2
matching.obj <- matchit(ps.formula,
data = analytic11n,
method = "nearest",
ratio = 1,
caliper = .2*sd(logitPS))
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
# see how many matched
matching.obj
#> A `matchit` object
#> - method: 1:1 nearest neighbor matching without replacement
#> - distance: Propensity score [caliper]
#>
#> - estimated with logistic regression
#> - caliper: <distance> (0.015)
#> - number of obs.: 1424 (original), 128 (matched)
#> - target estimand: ATT
#> - covariates: age, sex, stress, married, income, race, bmi, phyact, smoke, doctor, drink, bp, immigrate, fruit, diab, edu
OACVD.match <- match.data(matching.obj)# Step 3
by(OACVD.match$distance, OACVD.match$OA, summary)
#> OACVD.match$OA: 0
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.004671 0.041740 0.094963 0.124665 0.184103 0.418206
#> ------------------------------------------------------------
#> OACVD.match$OA: 1
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.004671 0.041694 0.095089 0.125262 0.183739 0.424895
tab1 <- CreateTableOne(strata = "OA", data = OACVD.match,
test = FALSE, vars = var.names)
print(tab1, smd = TRUE)
#> Stratified by OA
#> 0 1 SMD
#> n 64 64
#> age (%) 0.196
#> 20-29 years 4 ( 6.2) 4 ( 6.2)
#> 30-39 years 16 (25.0) 11 (17.2)
#> 40-49 years 16 (25.0) 18 (28.1)
#> 50-59 years 25 (39.1) 28 (43.8)
#> 60-64 years 3 ( 4.7) 3 ( 4.7)
#> 65 years and over 0 ( 0.0) 0 ( 0.0)
#> teen 0 ( 0.0) 0 ( 0.0)
#> sex = Male (%) 27 (42.2) 30 (46.9) 0.094
#> stress = stressed (%) 18 (28.1) 18 (28.1) <0.001
#> married = single (%) 21 (32.8) 23 (35.9) 0.066
#> income (%) 0.204
#> $29,999 or less 11 (17.2) 13 (20.3)
#> $30,000-$49,999 19 (29.7) 14 (21.9)
#> $50,000-$79,999 13 (20.3) 12 (18.8)
#> $80,000 or more 21 (32.8) 25 (39.1)
#> race = White (%) 40 (62.5) 42 (65.6) 0.065
#> bmi (%) <0.001
#> Underweight 0 ( 0.0) 0 ( 0.0)
#> healthy weight 18 (28.1) 18 (28.1)
#> Overweight 46 (71.9) 46 (71.9)
#> phyact (%) 0.096
#> Active 14 (21.9) 16 (25.0)
#> Inactive 39 (60.9) 36 (56.2)
#> Moderate 11 (17.2) 12 (18.8)
#> smoke (%) 0.267
#> Never smoker 14 (21.9) 9 (14.1)
#> Current smoker 19 (29.7) 26 (40.6)
#> Former smoker 31 (48.4) 29 (45.3)
#> doctor = Yes (%) 48 (75.0) 44 (68.8) 0.139
#> drink (%) 0.123
#> Never drank 2 ( 3.1) 2 ( 3.1)
#> Current drinker 52 (81.2) 49 (76.6)
#> Former driker 10 (15.6) 13 (20.3)
#> bp = Yes (%) 7 (10.9) 5 ( 7.8) 0.107
#> immigrate (%) 0.260
#> not immigrant 62 (96.9) 58 (90.6)
#> > 10 years 2 ( 3.1) 6 ( 9.4)
#> recent 0 ( 0.0) 0 ( 0.0)
#> fruit (%) 0.116
#> 0-3 daily serving 19 (29.7) 19 (29.7)
#> 4-6 daily serving 27 (42.2) 30 (46.9)
#> 6+ daily serving 18 (28.1) 15 (23.4)
#> diab = Yes (%) 0 ( 0.0) 3 ( 4.7) 0.314
#> edu (%) 0.108
#> < 2ndary 14 (21.9) 13 (20.3)
#> 2nd grad. 1 ( 1.6) 2 ( 3.1)
#> Other 2nd grad. 1 ( 1.6) 1 ( 1.6)
#> Post-2nd grad. 48 (75.0) 48 (75.0)Question for the students
- Did all of the SMDs decrease?
Look at the data
Step 4
Estimate treatment effect for matched data
Different models (e.g., unconditional logistic regression, survey design) are fitted to estimate the treatment effect in the matched sample.
Unconditional logistic
Survey design
Convert data to design
The matched data is converted to a survey design object to account for the matched pairs in the analysis.
analytic.miss$matched <- 0
length(analytic.miss$ID) # full data
#> [1] 397173
length(OACVD.match$ID) # matched data
#> [1] 128
length(analytic.miss$ID[analytic.miss$ID %in% OACVD.match$ID])
#> [1] 128
analytic.miss$matched[analytic.miss$ID %in% OACVD.match$ID] <- 1
table(analytic.miss$matched)
#>
#> 0 1
#> 397045 128
w.design0 <- svydesign(id=~1, weights=~survey.weight,
data=analytic.miss)
w.design.m <- subset(w.design0, matched == 1)Balance in matched population?
tab1 <- svyCreateTableOne(strata = "OA", data = w.design.m,
test = FALSE, vars = var.names)
print(tab1, smd = TRUE)
#> Stratified by OA
#> 0 1 SMD
#> n 1783.6 2002.1
#> age (%) 0.307
#> 20-29 years 131.0 ( 7.3) 120.9 ( 6.0)
#> 30-39 years 388.0 (21.8) 237.8 (11.9)
#> 40-49 years 518.3 (29.1) 572.7 (28.6)
#> 50-59 years 680.1 (38.1) 999.3 (49.9)
#> 60-64 years 66.1 ( 3.7) 71.4 ( 3.6)
#> 65 years and over 0.0 ( 0.0) 0.0 ( 0.0)
#> teen 0.0 ( 0.0) 0.0 ( 0.0)
#> sex = Male (%) 852.4 (47.8) 985.1 (49.2) 0.028
#> stress = stressed (%) 544.6 (30.5) 531.8 (26.6) 0.088
#> married = single (%) 419.8 (23.5) 427.5 (21.4) 0.052
#> income (%) 0.222
#> $29,999 or less 266.6 (14.9) 352.4 (17.6)
#> $30,000-$49,999 462.8 (25.9) 348.8 (17.4)
#> $50,000-$79,999 298.6 (16.7) 315.7 (15.8)
#> $80,000 or more 755.5 (42.4) 985.2 (49.2)
#> race = White (%) 1129.2 (63.3) 1364.9 (68.2) 0.103
#> bmi (%) 0.045
#> Underweight 0.0 ( 0.0) 0.0 ( 0.0)
#> healthy weight 483.3 (27.1) 583.3 (29.1)
#> Overweight 1300.2 (72.9) 1418.8 (70.9)
#> phyact (%) 0.054
#> Active 448.0 (25.1) 493.9 (24.7)
#> Inactive 1075.2 (60.3) 1176.6 (58.8)
#> Moderate 260.3 (14.6) 331.5 (16.6)
#> smoke (%) 0.288
#> Never smoker 400.2 (22.4) 265.8 (13.3)
#> Current smoker 548.8 (30.8) 836.6 (41.8)
#> Former smoker 834.6 (46.8) 899.6 (44.9)
#> doctor = Yes (%) 1376.0 (77.1) 1430.1 (71.4) 0.131
#> drink (%) 0.194
#> Never drank 44.0 ( 2.5) 112.6 ( 5.6)
#> Current drinker 1464.1 (82.1) 1510.6 (75.5)
#> Former driker 275.4 (15.4) 378.9 (18.9)
#> bp = Yes (%) 166.6 ( 9.3) 153.5 ( 7.7) 0.060
#> immigrate (%) 0.235
#> not immigrant 1694.8 (95.0) 1774.1 (88.6)
#> > 10 years 88.8 ( 5.0) 228.0 (11.4)
#> recent 0.0 ( 0.0) 0.0 ( 0.0)
#> fruit (%) 0.293
#> 0-3 daily serving 426.1 (23.9) 480.8 (24.0)
#> 4-6 daily serving 748.1 (41.9) 1082.3 (54.1)
#> 6+ daily serving 609.4 (34.2) 439.0 (21.9)
#> diab = Yes (%) 0.0 ( 0.0) 83.6 ( 4.2) 0.295
#> edu (%) 0.172
#> < 2ndary 324.9 (18.2) 342.8 (17.1)
#> 2nd grad. 18.8 ( 1.1) 47.6 ( 2.4)
#> Other 2nd grad. 15.2 ( 0.9) 52.2 ( 2.6)
#> Post-2nd grad. 1424.7 (79.9) 1559.4 (77.9)Outcome analysis
Matched data with increase ratio
The matching process is repeated with a different ratio (e.g., 1:5) to explore how changing the ratio affects the covariate balance and treatment effect estimation.
# Step 1 and 2
matching.obj <- matchit(ps.formula,
data = analytic11n,
method = "nearest",
ratio = 5,
caliper = 0.2)
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
# see how many matched
matching.obj
#> A `matchit` object
#> - method: 5:1 nearest neighbor matching without replacement
#> - distance: Propensity score [caliper]
#>
#> - estimated with logistic regression
#> - caliper: <distance> (0.013)
#> - number of obs.: 1424 (original), 349 (matched)
#> - target estimand: ATT
#> - covariates: age, sex, stress, married, income, race, bmi, phyact, smoke, doctor, drink, bp, immigrate, fruit, diab, edu
OACVD.match <- match.data(matching.obj)
# Step 3
by(OACVD.match$distance, OACVD.match$OA, summary)
#> OACVD.match$OA: 0
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.004643 0.039181 0.084421 0.101576 0.146403 0.418206
#> ------------------------------------------------------------
#> OACVD.match$OA: 1
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.004671 0.041694 0.095089 0.125262 0.183739 0.424895
tab1 <- CreateTableOne(strata = "OA", data = OACVD.match,
test = FALSE, vars = var.names)
print(tab1, smd = TRUE)
#> Stratified by OA
#> 0 1 SMD
#> n 285 64
#> age (%) 0.217
#> 20-29 years 24 ( 8.4) 4 ( 6.2)
#> 30-39 years 59 (20.7) 11 (17.2)
#> 40-49 years 94 (33.0) 18 (28.1)
#> 50-59 years 98 (34.4) 28 (43.8)
#> 60-64 years 10 ( 3.5) 3 ( 4.7)
#> 65 years and over 0 ( 0.0) 0 ( 0.0)
#> teen 0 ( 0.0) 0 ( 0.0)
#> sex = Male (%) 132 (46.3) 30 (46.9) 0.011
#> stress = stressed (%) 81 (28.4) 18 (28.1) 0.007
#> married = single (%) 91 (31.9) 23 (35.9) 0.085
#> income (%) 0.065
#> $29,999 or less 64 (22.5) 13 (20.3)
#> $30,000-$49,999 65 (22.8) 14 (21.9)
#> $50,000-$79,999 51 (17.9) 12 (18.8)
#> $80,000 or more 105 (36.8) 25 (39.1)
#> race = White (%) 169 (59.3) 42 (65.6) 0.131
#> bmi (%) 0.097
#> Underweight 0 ( 0.0) 0 ( 0.0)
#> healthy weight 68 (23.9) 18 (28.1)
#> Overweight 217 (76.1) 46 (71.9)
#> phyact (%) 0.136
#> Active 57 (20.0) 16 (25.0)
#> Inactive 178 (62.5) 36 (56.2)
#> Moderate 50 (17.5) 12 (18.8)
#> smoke (%) 0.097
#> Never smoker 46 (16.1) 9 (14.1)
#> Current smoker 123 (43.2) 26 (40.6)
#> Former smoker 116 (40.7) 29 (45.3)
#> doctor = Yes (%) 183 (64.2) 44 (68.8) 0.096
#> drink (%) 0.051
#> Never drank 10 ( 3.5) 2 ( 3.1)
#> Current drinker 212 (74.4) 49 (76.6)
#> Former driker 63 (22.1) 13 (20.3)
#> bp = Yes (%) 22 ( 7.7) 5 ( 7.8) 0.003
#> immigrate (%) 0.100
#> not immigrant 266 (93.3) 58 (90.6)
#> > 10 years 19 ( 6.7) 6 ( 9.4)
#> recent 0 ( 0.0) 0 ( 0.0)
#> fruit (%) 0.149
#> 0-3 daily serving 104 (36.5) 19 (29.7)
#> 4-6 daily serving 124 (43.5) 30 (46.9)
#> 6+ daily serving 57 (20.0) 15 (23.4)
#> diab = Yes (%) 12 ( 4.2) 3 ( 4.7) 0.023
#> edu (%) 0.137
#> < 2ndary 67 (23.5) 13 (20.3)
#> 2nd grad. 9 ( 3.2) 2 ( 3.1)
#> Other 2nd grad. 9 ( 3.2) 1 ( 1.6)
#> Post-2nd grad. 200 (70.2) 48 (75.0)Question for the students
- Did all of the SMDs decrease?
Look at the data
Combining matching weights
Different approaches to incorporating weights (e.g., matching weights, survey weights) are explored.
Not incorporating matching weights
analytic.miss$matched <- 0
length(analytic.miss$ID) # full data
#> [1] 397173
length(OACVD.match$ID) # matched data
#> [1] 349
length(analytic.miss$ID[analytic.miss$ID %in% OACVD.match$ID])
#> [1] 349
analytic.miss$matched[analytic.miss$ID %in% OACVD.match$ID] <- 1
table(analytic.miss$matched)
#>
#> 0 1
#> 396824 349
w.design0 <- svydesign(id=~1, weights=~survey.weight,
data=analytic.miss)
w.design.m <- subset(w.design0, matched == 1)Incorporating matching weights
analytic.miss$matched <- 0
length(analytic.miss$ID) # full data
#> [1] 397173
length(OACVD.match$ID) # matched data
#> [1] 349
length(analytic.miss$ID[analytic.miss$ID %in% OACVD.match$ID])
#> [1] 349
analytic.miss$matched[analytic.miss$ID %in% OACVD.match$ID] <- 1
table(analytic.miss$matched)
#>
#> 0 1
#> 396824 349# multiply with matching (ratio) weights with survey weights
analytic.miss$combined.weight <- 0
analytic.miss$combined.weight[analytic.miss$ID %in% OACVD.match$ID] <-
OACVD.match$weights*OACVD.match$survey.weight
w.design0 <- svydesign(id=~1, weights=~combined.weight,
data=analytic.miss)
w.design.m <- subset(w.design0, matched == 1)Matched with replacement
Matching is performed with replacement, allowing control units to be used in more than one match.
# Step 1 and 2
matching.obj <- matchit(ps.formula,
data = analytic11n,
method = "nearest",
ratio = 5,
caliper = 0.2,
replace = TRUE)
#> Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
# see how many matched
matching.obj
#> A `matchit` object
#> - method: 5:1 nearest neighbor matching with replacement
#> - distance: Propensity score [caliper]
#>
#> - estimated with logistic regression
#> - caliper: <distance> (0.013)
#> - number of obs.: 1424 (original), 308 (matched)
#> - target estimand: ATT
#> - covariates: age, sex, stress, married, income, race, bmi, phyact, smoke, doctor, drink, bp, immigrate, fruit, diab, edu
OACVD.match <- match.data(matching.obj)
# Step 3
by(OACVD.match$distance, OACVD.match$OA, summary)
#> OACVD.match$OA: 0
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.004643 0.034244 0.067224 0.100844 0.148958 0.418206
#> ------------------------------------------------------------
#> OACVD.match$OA: 1
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> 0.004671 0.042322 0.097877 0.129743 0.189256 0.424895
tab1 <- CreateTableOne(strata = "OA", data = OACVD.match,
test = FALSE, vars = var.names)
print(tab1, smd = TRUE)
#> Stratified by OA
#> 0 1 SMD
#> n 243 65
#> age (%) 0.266
#> 20-29 years 22 ( 9.1) 4 ( 6.2)
#> 30-39 years 57 (23.5) 11 (16.9)
#> 40-49 years 74 (30.5) 18 (27.7)
#> 50-59 years 82 (33.7) 29 (44.6)
#> 60-64 years 8 ( 3.3) 3 ( 4.6)
#> 65 years and over 0 ( 0.0) 0 ( 0.0)
#> teen 0 ( 0.0) 0 ( 0.0)
#> sex = Male (%) 113 (46.5) 31 (47.7) 0.024
#> stress = stressed (%) 67 (27.6) 19 (29.2) 0.037
#> married = single (%) 75 (30.9) 23 (35.4) 0.096
#> income (%) 0.079
#> $29,999 or less 53 (21.8) 13 (20.0)
#> $30,000-$49,999 57 (23.5) 14 (21.5)
#> $50,000-$79,999 44 (18.1) 12 (18.5)
#> $80,000 or more 89 (36.6) 26 (40.0)
#> race = White (%) 146 (60.1) 42 (64.6) 0.094
#> bmi (%) 0.088
#> Underweight 0 ( 0.0) 0 ( 0.0)
#> healthy weight 58 (23.9) 18 (27.7)
#> Overweight 185 (76.1) 47 (72.3)
#> phyact (%) 0.160
#> Active 45 (18.5) 16 (24.6)
#> Inactive 155 (63.8) 37 (56.9)
#> Moderate 43 (17.7) 12 (18.5)
#> smoke (%) 0.095
#> Never smoker 40 (16.5) 9 (13.8)
#> Current smoker 101 (41.6) 26 (40.0)
#> Former smoker 102 (42.0) 30 (46.2)
#> doctor = Yes (%) 152 (62.6) 45 (69.2) 0.141
#> drink (%) 0.059
#> Never drank 9 ( 3.7) 2 ( 3.1)
#> Current drinker 181 (74.5) 50 (76.9)
#> Former driker 53 (21.8) 13 (20.0)
#> bp = Yes (%) 19 ( 7.8) 5 ( 7.7) 0.005
#> immigrate (%) 0.115
#> not immigrant 228 (93.8) 59 (90.8)
#> > 10 years 15 ( 6.2) 6 ( 9.2)
#> recent 0 ( 0.0) 0 ( 0.0)
#> fruit (%) 0.147
#> 0-3 daily serving 87 (35.8) 19 (29.2)
#> 4-6 daily serving 109 (44.9) 31 (47.7)
#> 6+ daily serving 47 (19.3) 15 (23.1)
#> diab = Yes (%) 11 ( 4.5) 3 ( 4.6) 0.004
#> edu (%) 0.175
#> < 2ndary 58 (23.9) 13 (20.0)
#> 2nd grad. 8 ( 3.3) 2 ( 3.1)
#> Other 2nd grad. 9 ( 3.7) 1 ( 1.5)
#> Post-2nd grad. 168 (69.1) 49 (75.4)Question for the students
- Did all of the SMDs decrease?
Look at the data
Survey design
The matched data is converted into a survey design object, and the treatment effect is estimated while accounting for the complex survey design.
analytic.miss$matched <- 0
length(analytic.miss$ID) # full data
#> [1] 397173
length(OACVD.match$ID) # matched data
#> [1] 308
length(analytic.miss$ID[analytic.miss$ID %in% OACVD.match$ID])
#> [1] 308
analytic.miss$matched[analytic.miss$ID %in% OACVD.match$ID] <- 1
table(analytic.miss$matched)
#>
#> 0 1
#> 396865 308# multiply with matching (ratio) weights with survey weights
analytic.miss$combined.weight <- 0
analytic.miss$combined.weight[analytic.miss$ID %in% OACVD.match$ID] <-
OACVD.match$weights*OACVD.match$survey.weight
w.design0 <- svydesign(id=~1, weights=~combined.weight,
data=analytic.miss)
w.design.m <- subset(w.design0, matched == 1)Video content (optional)
For those who prefer a video walkthrough, feel free to watch the video below, which offers a description of an earlier version of the above content.