13  Refined Results

Reviewed the current literature on selection of candidate learners to understand why TMLE was not achieving best coverage (particularly double cross-fitted version).

(Naimi, Mishler, and Kennedy 2021; Balzer and Westling 2021; Phillips et al. 2023; Zivich and Breskin 2021)

Donsker class and Smooth learner

• Donsker class: uniform convergence of empirical processes, generalization performance of learning algorithms, reduction of the risk of overfitting
• Smooth learner: algorithm producing differentiable and continuous functions. Non-smooth are often sensitive to small changes in the training data and can overfit easily.

1. Logistic regression: smooth learner, belongs to the Donsker class
2. MARS: piecewise smooth learner, classification of MARS into the Donsker class is not straightforward
3. LASSO: produces a continuous function, can be considered piecewise smooth or quasi-smooth; can belong to the Donsker class
4. XGBoost: non-smooth learner, classification of XGBoost into the Donsker class is not straightforward

Super Learner guidelines suggested using diverse learners, including both smooth and non-smooth learners. The main idea behind this recommendation was to leverage the strengths of different learners and allow them to compensate for each other’s weaknesses. By combining diverse base learners, Super Learner aims to improve the overall generalization performance of the ensemble. However, researchers and practitioners have gained a deeper understanding of the implications of including non-smooth learners in the ensemble. The potential downsides of non-smooth learners, such as high variance and overfitting, are now better understood. As a result, more emphasis may be placed on carefully selecting and tuning non-smooth learners to minimize their potential negative impact on the ensemble’s performance.

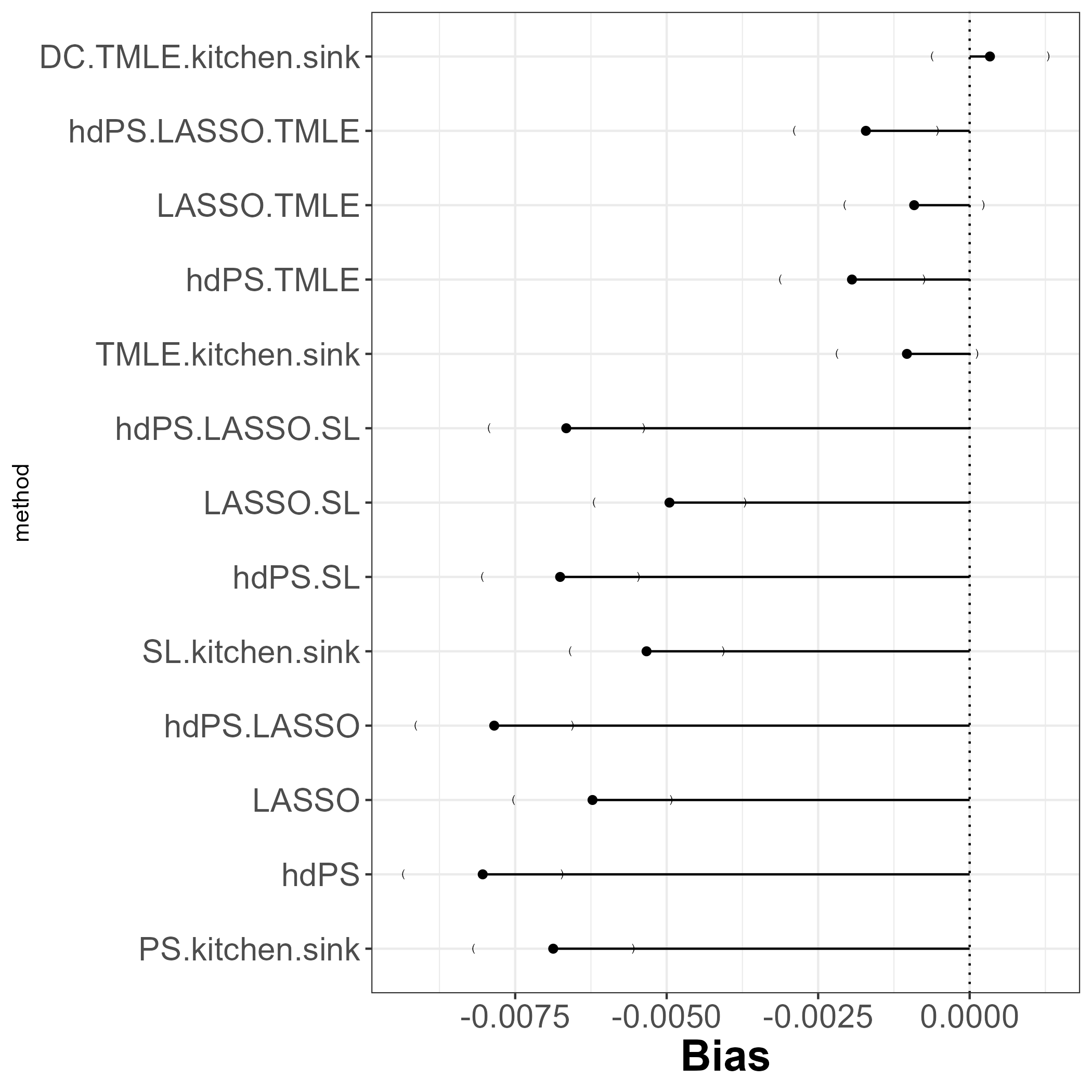
13.1 Bias

• SL represents those where super learner was used with the following 3 candidate learners
  1. Logistic regression
  2. MARS (Multivariate Adaptive Regression Splines)
  3. LASSO
• TMLE represents those where TMLE was used
• DC represents double cross-fit.

XGBoost omitted

• DC version of TMLE (kitchen sink) associated with least bias!
• Non-super learner methods remains the same (results did not change).
• Same super learner used for SL and TMLE methods.

13.2 MSE

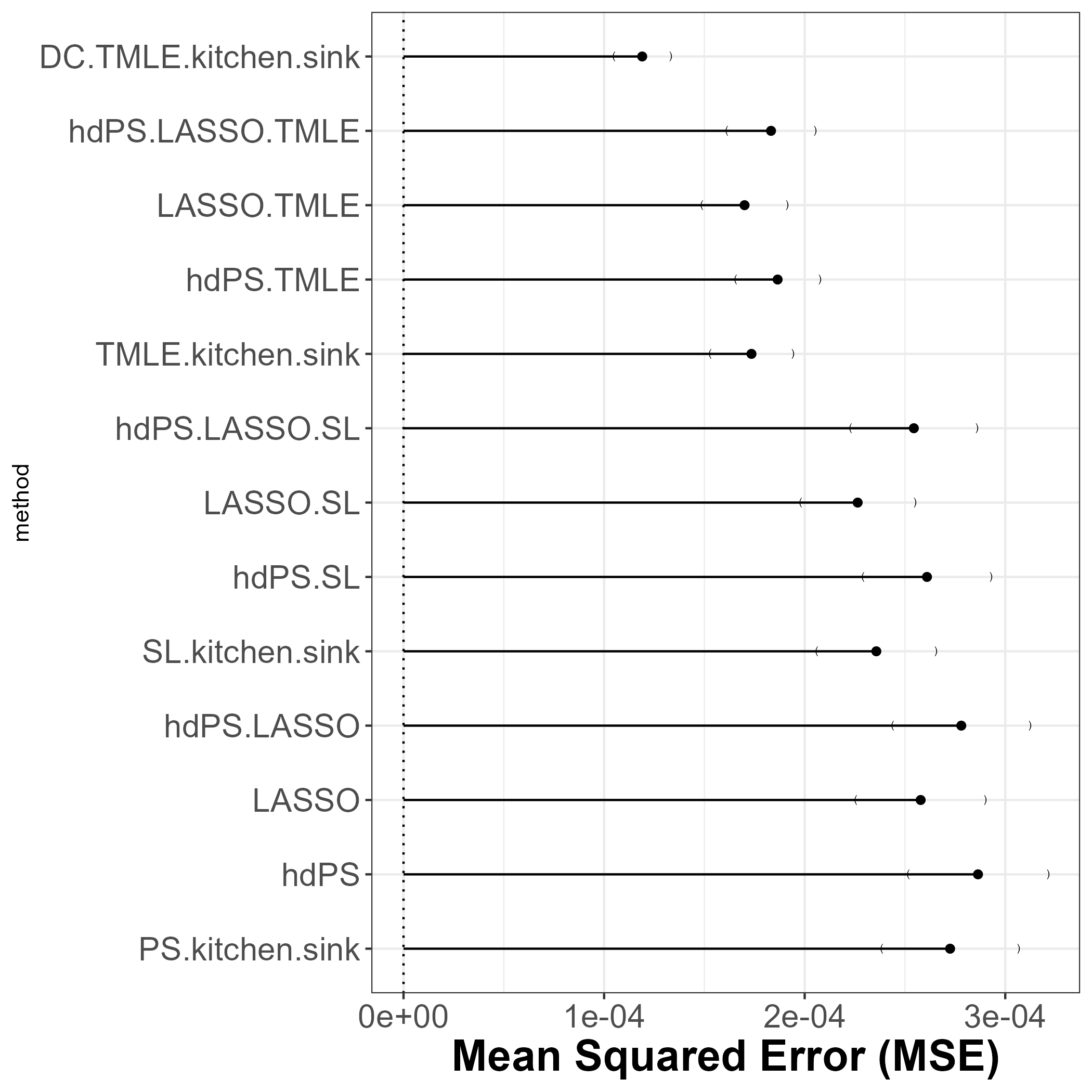
• DC version of TMLE (kitchen sink) associated with least MSE!

13.3 Relative Error

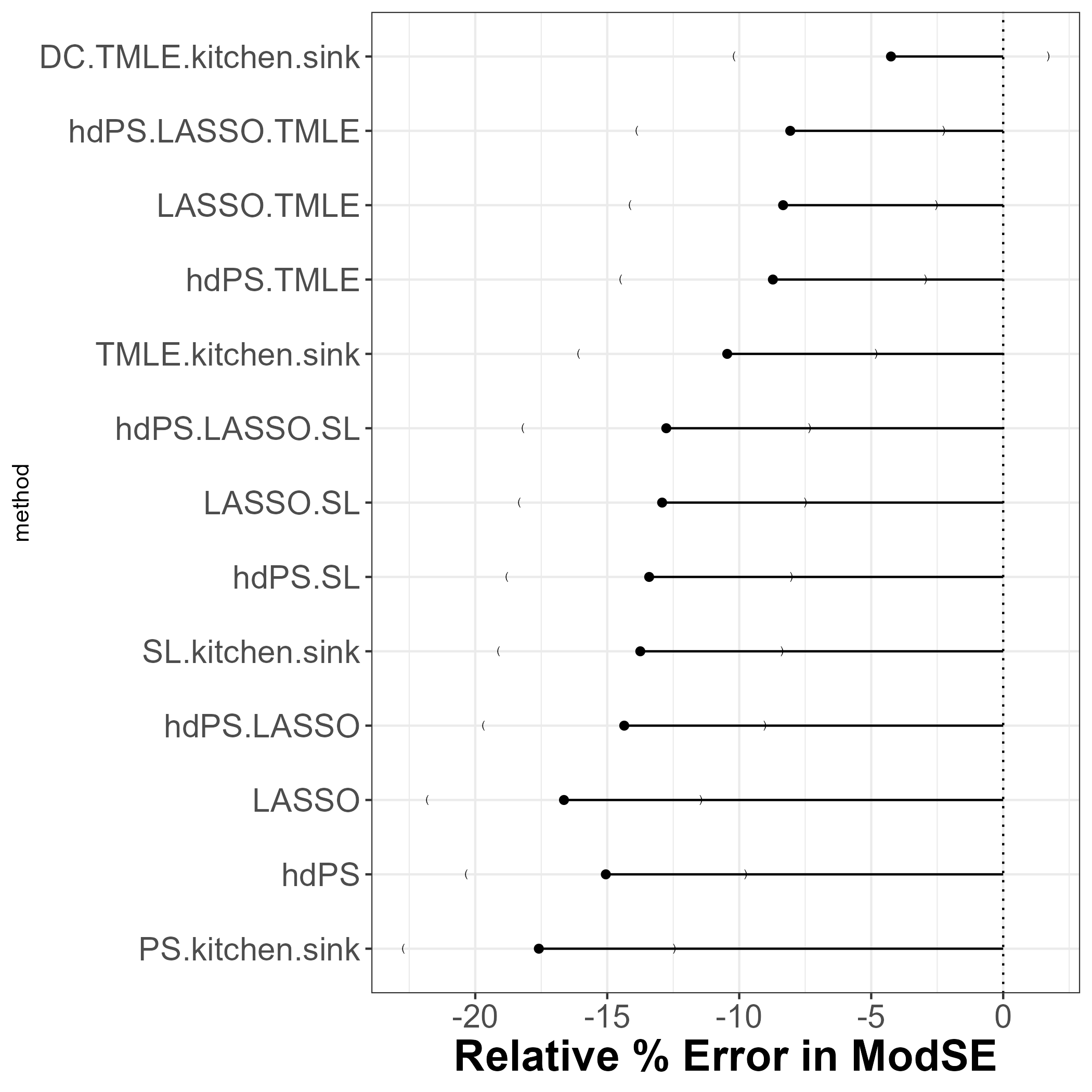
• DC version of TMLE (kitchen sink) associated with least relative error in model SE estimation!

13.4 Coverage

• DC version of TMLE (kitchen sink) associated with coverage closest to nominal!

13.5 Bias eliminated coverage

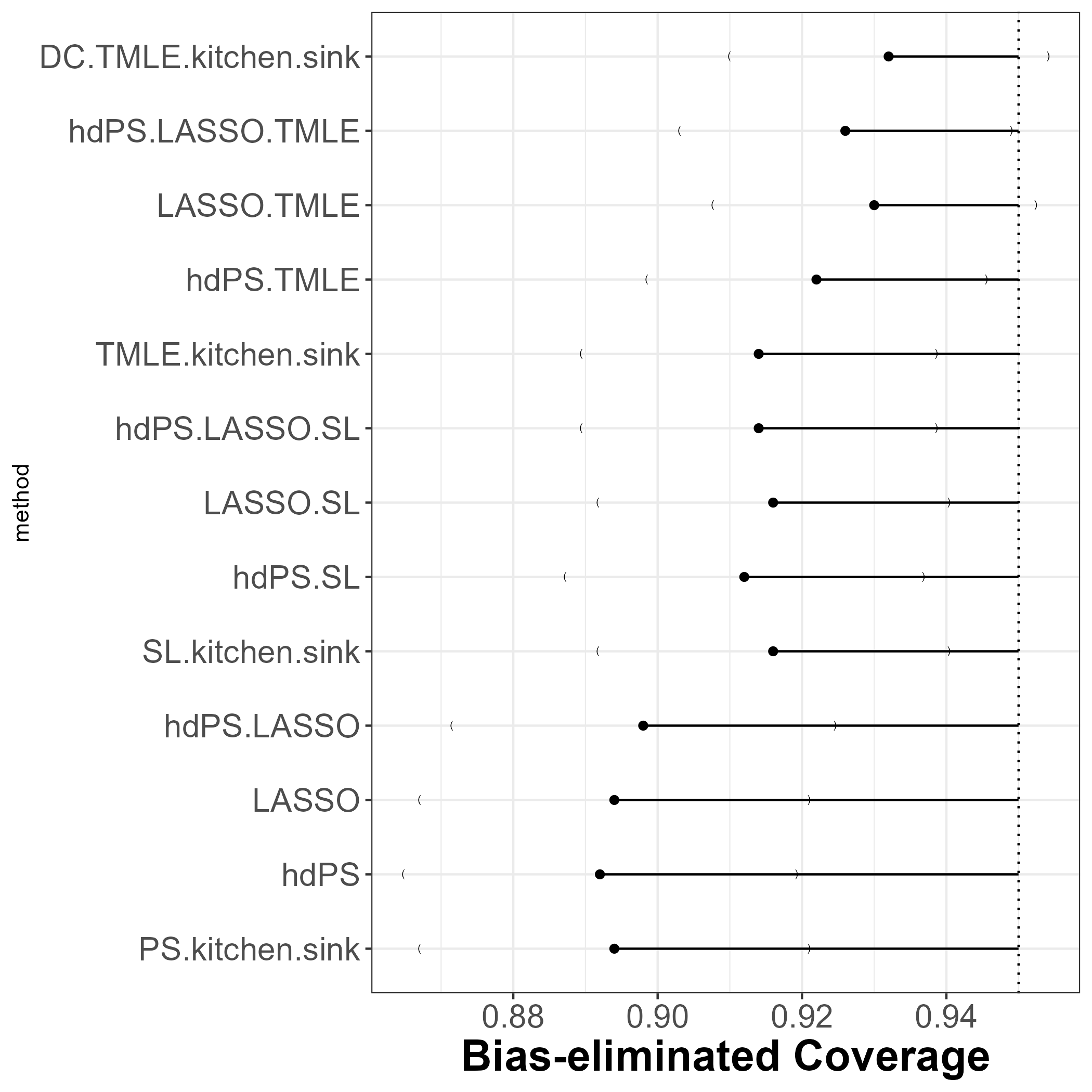
• DC version of TMLE (kitchen sink) associated with bias eliminated coverage closest to nominal!

13.6 More Details

Review more detailed simulation results conducted:

Analysis strategy	Outcome Model Specification
Firth regression	The same
Stabilized weights	The same
Various outcome model specification
	No covariate adjustment
	Just investigator-specified covariate adjustment
	Adjustment of only those investigator-specified covariates that are imbalanced (SMD > 0.1)
	Adjustment of only those covariates that are imbalanced (SMD > 0.1; investigator-specified or recurrence)
	Adjustment of all covariates (investigator-specified or recurrence)

(Firth 1993; Austin and Stuart 2015)

All of the aove figures are based on adjustment of all covariates (investigator-specified or recurrence) in the outcome model.

ShinyApp

Look at the ShinyApp for additional details!

Austin, Peter C, and Elizabeth A Stuart. 2015. “Moving Towards Best Practice When Using Inverse Probability of Treatment Weighting (IPTW) Using the Propensity Score to Estimate Causal Treatment Effects in Observational Studies.” Statistics in Medicine 34 (28): 3661–79.

Balzer, Laura B, and Ted Westling. 2021. “Demystifying Statistical Inference When Using Machine Learning in Causal Research.” American Journal of Epidemiology. https://doi.org/10.1093/aje/kwab200.

Firth, David. 1993. “Bias Reduction of Maximum Likelihood Estimates.” Biometrika 80 (1): 27–38.

Naimi, Ashley I, Alan E Mishler, and Edward H Kennedy. 2021. “Challenges in Obtaining Valid Causal Effect Estimates with Machine Learning Algorithms.” American Journal of Epidemiology. https://doi.org/10.1093/aje/kwab201.

Phillips, Rachael V, Mark J van der Laan, Hana Lee, and Susan Gruber. 2023. “Practical Considerations for Specifying a Super Learner.” International Journal of Epidemiology. https://doi.org/10.1093/ije/dyad023.

Zivich, Paul N, and Alexander Breskin. 2021. “Machine Learning for Causal Inference: On the Use of Cross-Fit Estimators.” Epidemiology (Cambridge, Mass.) 32 (3): 393.