Chapter 6 Supervised Learning

In this chapter, we will move beyond statistical regression, and introduce some of the popular machine learning methods.

Watch the video describing this chapter - I
Watch the video describing this chapters -II

6.1 Read previously saved data

ObsData <- readRDS(file = "data/rhcAnalytic.RDS")
levels(ObsData$Death)=c("No","Yes")
out.formula1 <- readRDS(file = "data/form1.RDS")
out.formula2 <- readRDS(file = "data/form2.RDS")

6.2 Continuous outcome

6.2.1 Cross-validation LASSO

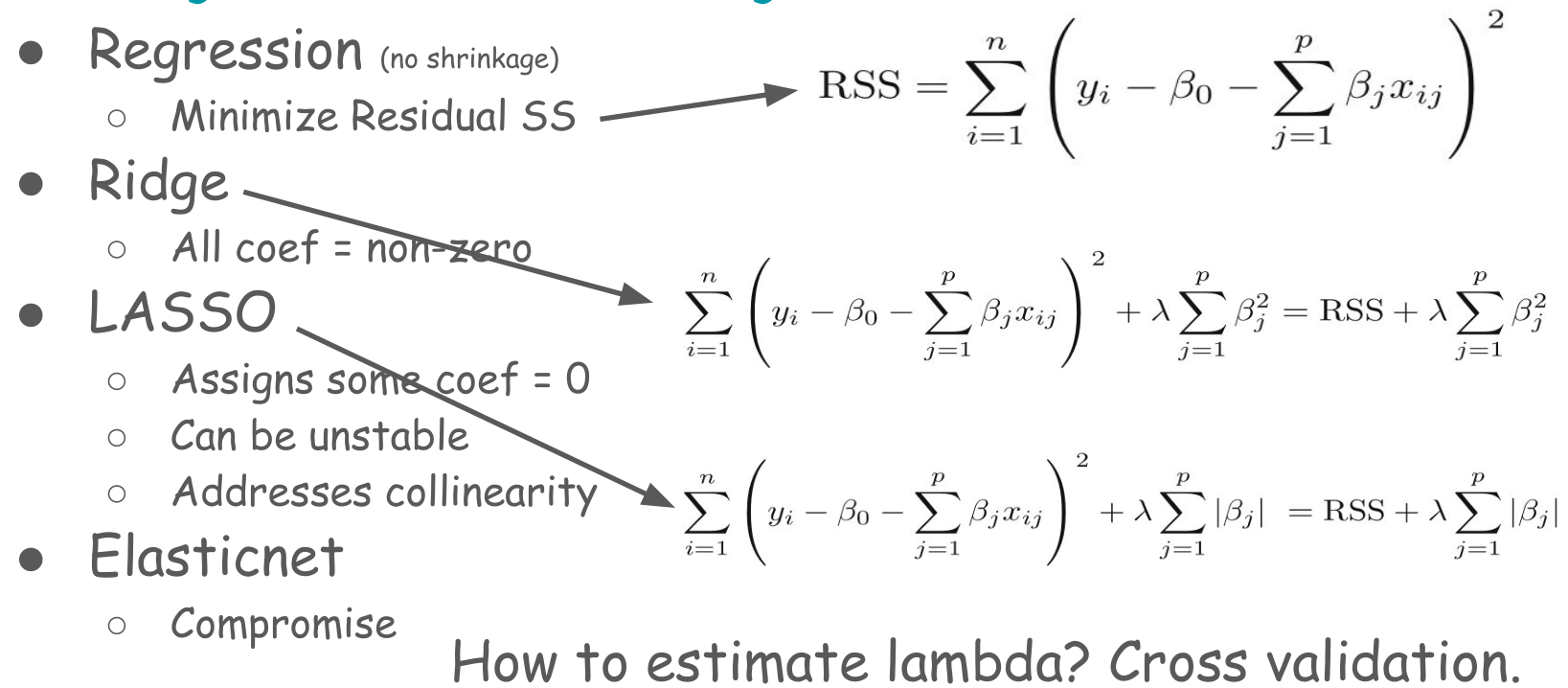
ctrl <- trainControl(method = "cv", number = 5)
fit.cv.con <- train(out.formula1, trControl = ctrl,
               data = ObsData, method = "glmnet",
               lambda= 0,
               tuneGrid = expand.grid(alpha = 1,  
                                      lambda = 0),
               verbose = FALSE)
fit.cv.con

## glmnet 
## 
## 5735 samples
##   50 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 4587, 4588, 4590, 4589, 4586 
## Resampling results:
## 
##   RMSE      Rsquared    MAE     
##   24.96631  0.05917659  15.21723
## 
## Tuning parameter 'alpha' was held constant at a value of 1
## Tuning
##  parameter 'lambda' was held constant at a value of 0

6.2.2 Cross-validation Ridge

ctrl <- trainControl(method = "cv", number = 5)
fit.cv.con <-train(out.formula1, trControl = ctrl,
               data = ObsData, method = "glmnet",
               lambda= 0,
               tuneGrid = expand.grid(alpha = 0,  
                                      lambda = 0),
               verbose = FALSE)
fit.cv.con

## glmnet 
## 
## 5735 samples
##   50 predictor
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 4588, 4588, 4588, 4588, 4588 
## Resampling results:
## 
##   RMSE      Rsquared    MAE     
##   25.12588  0.05561442  15.27411
## 
## Tuning parameter 'alpha' was held constant at a value of 0
## Tuning
##  parameter 'lambda' was held constant at a value of 0

6.3 Binary outcome

6.3.1 Cross-validation LASSO

ctrl<-trainControl(method = "cv", number = 5,
                   classProbs = TRUE,
                   summaryFunction = twoClassSummary)
fit.cv.bin<-train(out.formula2, trControl = ctrl,
               data = ObsData, method = "glmnet",
               lambda= 0,
               tuneGrid = expand.grid(alpha = 1,  
                                      lambda = 0),
               verbose = FALSE,
               metric="ROC")
fit.cv.bin

## glmnet 
## 
## 5735 samples
##   50 predictor
##    2 classes: 'No', 'Yes' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 4589, 4588, 4589, 4587, 4587 
## Resampling results:
## 
##   ROC        Sens       Spec     
##   0.7528523  0.4650087  0.8490056
## 
## Tuning parameter 'alpha' was held constant at a value of 1
## Tuning
##  parameter 'lambda' was held constant at a value of 0

Not okay to select variables from a shrinkage model, and then use them in a regular regression

6.3.2 Cross-validation Ridge

ctrl<-trainControl(method = "cv", number = 5,
                   classProbs = TRUE,
                   summaryFunction = twoClassSummary)
fit.cv.bin<-train(out.formula2, trControl = ctrl,
               data = ObsData, method = "glmnet",
               lambda= 0,
               tuneGrid = expand.grid(alpha = 0,  
                                      lambda = 0),
               verbose = FALSE,
               metric="ROC")
fit.cv.bin

## glmnet 
## 
## 5735 samples
##   50 predictor
##    2 classes: 'No', 'Yes' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 4589, 4587, 4587, 4589, 4588 
## Resampling results:
## 
##   ROC        Sens       Spec     
##   0.7560879  0.4649667  0.8573349
## 
## Tuning parameter 'alpha' was held constant at a value of 0
## Tuning
##  parameter 'lambda' was held constant at a value of 0

6.3.3 Cross-validation Elastic net

Alpha = mixing parameter
Lambda = regularization or tuning parameter
We can use expand.grid for model tuning

ctrl<-trainControl(method = "cv", number = 5,
                   classProbs = TRUE,
                   summaryFunction = twoClassSummary)
fit.cv.bin<-train(out.formula2, trControl = ctrl,
               data = ObsData, method = "glmnet",
               tuneGrid = expand.grid(alpha = seq(0.1,.2,by = 0.05),  
                                      lambda = seq(0.05,0.3,by = 0.05)),
               verbose = FALSE,
               metric="ROC")
fit.cv.bin

## glmnet 
## 
## 5735 samples
##   50 predictor
##    2 classes: 'No', 'Yes' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 4588, 4589, 4588, 4588, 4587 
## Resampling results across tuning parameters:
## 
##   alpha  lambda  ROC        Sens          Spec     
##   0.10   0.05    0.7500434  0.3686048665  0.8960186
##   0.10   0.10    0.7465449  0.2742108317  0.9395439
##   0.10   0.15    0.7417930  0.1738614619  0.9666829
##   0.10   0.20    0.7364791  0.0909077442  0.9868348
##   0.10   0.25    0.7294534  0.0243435428  0.9948954
##   0.10   0.30    0.7238117  0.0009925558  1.0000000
##   0.15   0.05    0.7489731  0.3482352505  0.9064964
##   0.15   0.10    0.7422912  0.2165808674  0.9524435
##   0.15   0.15    0.7331402  0.1023332469  0.9825359
##   0.15   0.20    0.7232533  0.0193745911  0.9954334
##   0.15   0.25    0.7164501  0.0000000000  1.0000000
##   0.15   0.30    0.7106881  0.0000000000  1.0000000
##   0.20   0.05    0.7476620  0.3308433021  0.9132132
##   0.20   0.10    0.7365773  0.1733664185  0.9658772
##   0.20   0.15    0.7229954  0.0402417194  0.9919395
##   0.20   0.20    0.7134900  0.0009925558  0.9997312
##   0.20   0.25    0.7073605  0.0000000000  1.0000000
##   0.20   0.30    0.6978155  0.0000000000  1.0000000
## 
## ROC was used to select the optimal model using the largest value.
## The final values used for the model were alpha = 0.1 and lambda = 0.05.

plot(fit.cv.bin)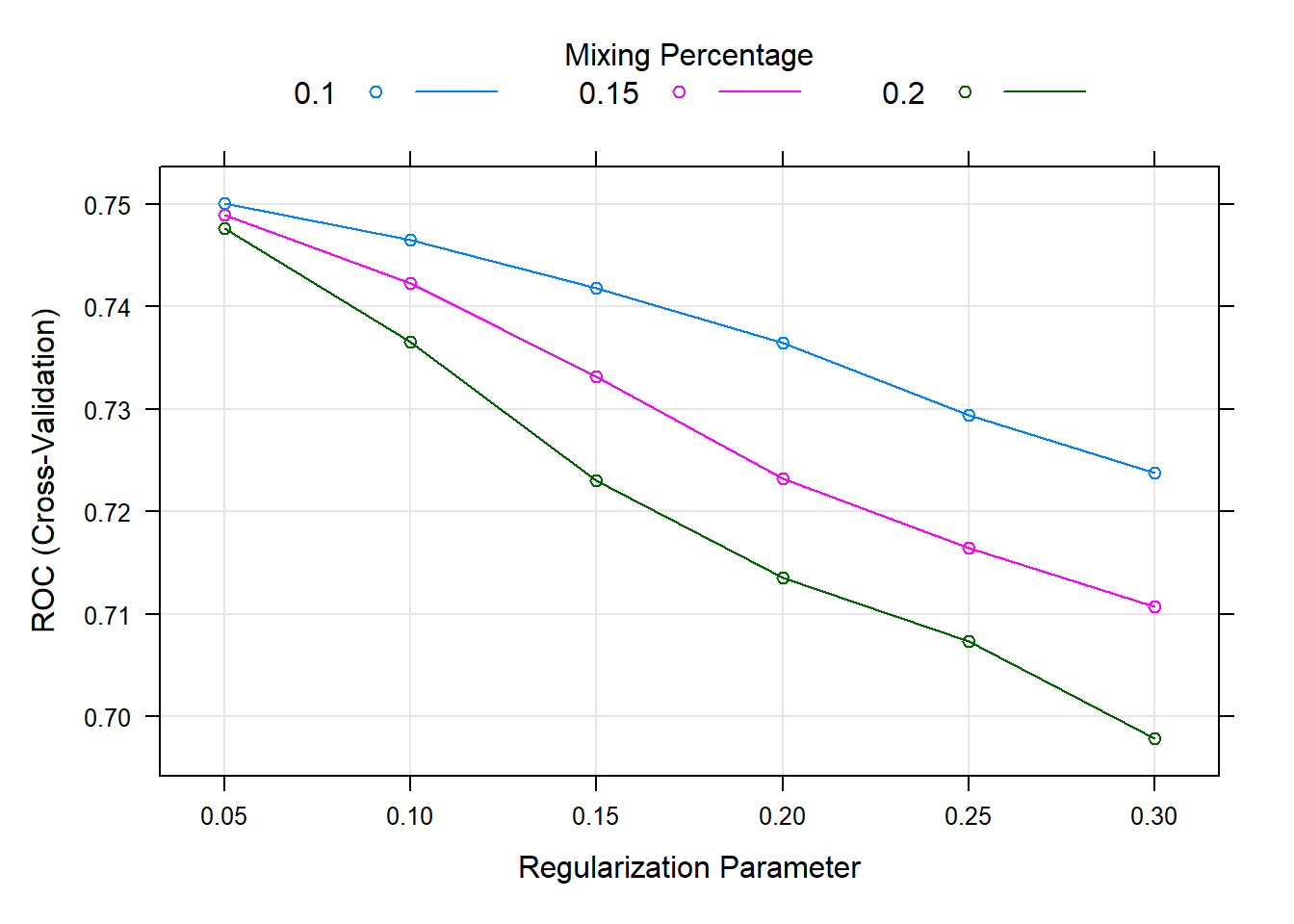

6.3.4 Decision tree

Decision tree
- Referred to as Classification and regression trees or CART
- Covers
  - Classification (categorical outcome)
  - Regression (continuous outcome)
- Flexible to incorporate non-linear effects automatically
  - No need to specify higher order terms / interactions
- Unstable, prone to overfitting, suffers from high variance

6.3.4.1 Simple CART

require(rpart)
summary(ObsData$DASIndex) # Duke Activity Status Index

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   11.00   16.06   19.75   20.50   23.43   33.00

cart.fit <- rpart(Death~DASIndex, data = ObsData)
par(mfrow = c(1,1), xpd = NA)
plot(cart.fit)
text(cart.fit, use.n = TRUE)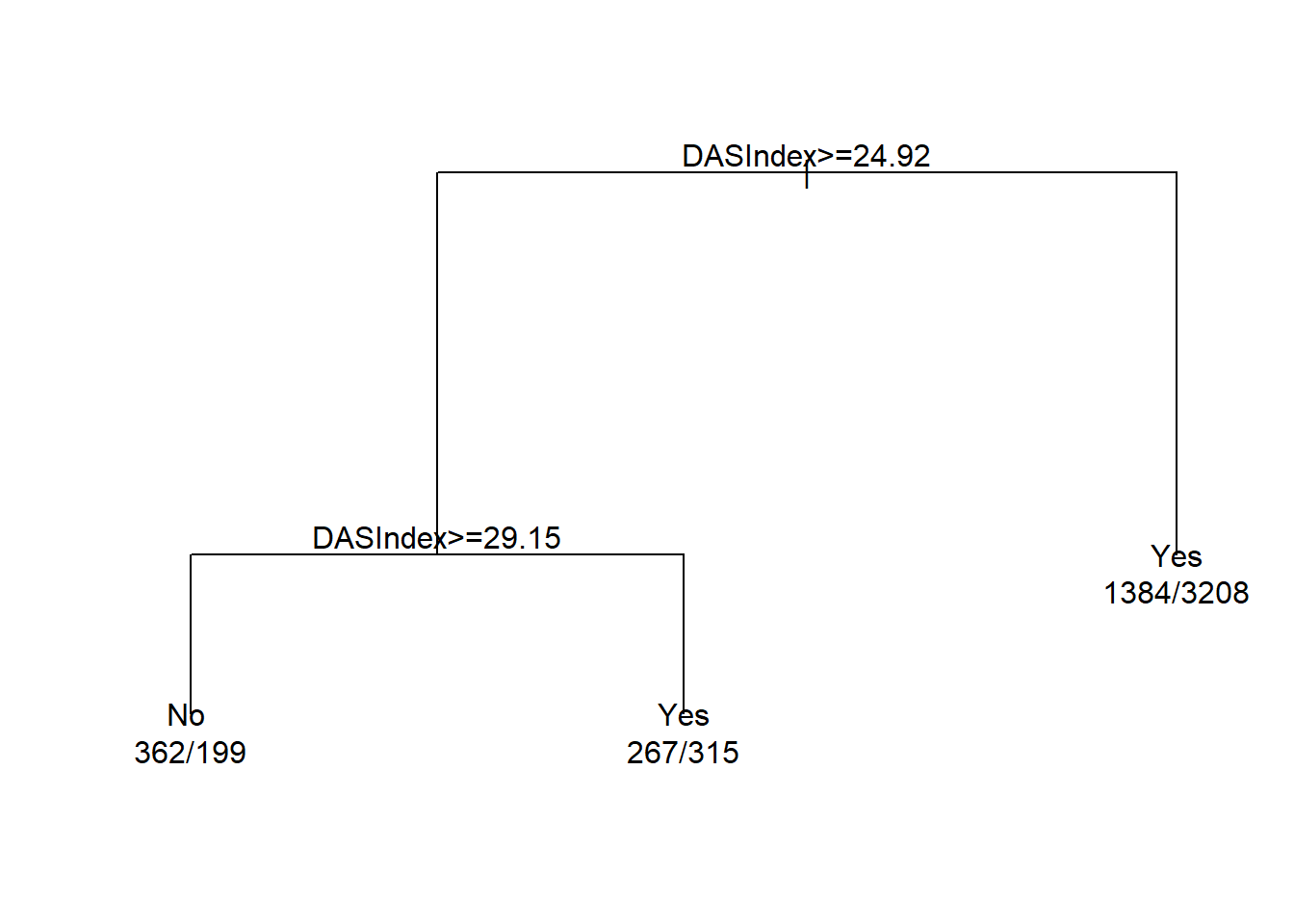

print(cart.fit)

## n= 5735 
## 
## node), split, n, loss, yval, (yprob)
##       * denotes terminal node
## 
## 1) root 5735 2013 Yes (0.3510026 0.6489974)  
##   2) DASIndex>=24.92383 1143  514 No (0.5503062 0.4496938)  
##     4) DASIndex>=29.14648 561  199 No (0.6452763 0.3547237) *
##     5) DASIndex< 29.14648 582  267 Yes (0.4587629 0.5412371) *
##   3) DASIndex< 24.92383 4592 1384 Yes (0.3013937 0.6986063) *

require(rattle)
require(rpart.plot)
require(RColorBrewer)
fancyRpartPlot(cart.fit, caption = NULL)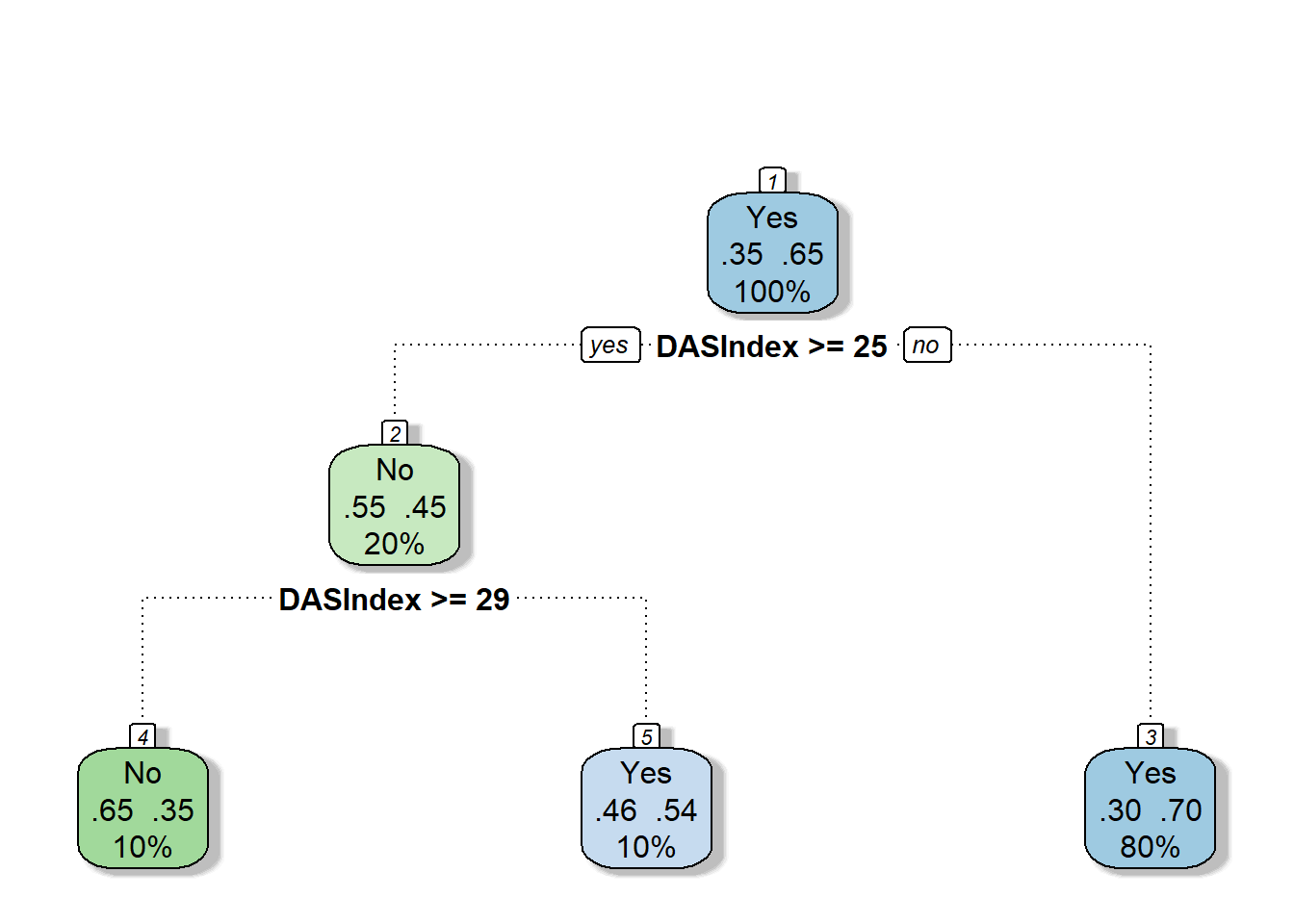

6.3.4.1.1 AUC

require(pROC)
obs.y2<-ObsData$Death
pred.y2 <- as.numeric(predict(cart.fit, type = "prob")[, 2])
rocobj <- roc(obs.y2, pred.y2)

## Setting levels: control = No, case = Yes

## Setting direction: controls < cases

rocobj

## 
## Call:
## roc.default(response = obs.y2, predictor = pred.y2)
## 
## Data: pred.y2 in 2013 controls (obs.y2 No) < 3722 cases (obs.y2 Yes).
## Area under the curve: 0.5981

plot(rocobj)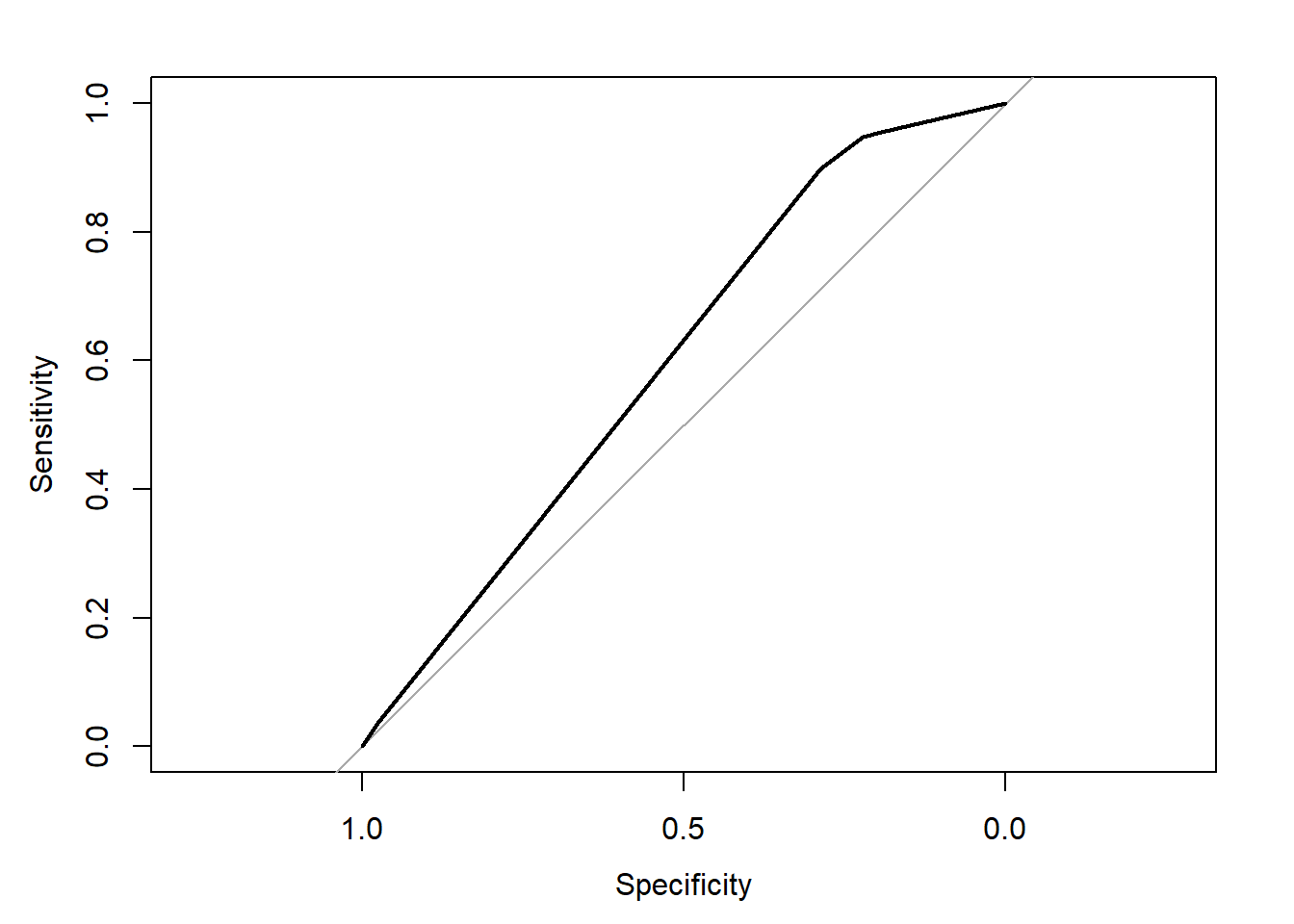

auc(rocobj)

## Area under the curve: 0.5981

6.3.4.2 Complex CART

More variables

out.formula2

## Death ~ Disease.category + Cancer + Cardiovascular + Congestive.HF + 
##     Dementia + Psychiatric + Pulmonary + Renal + Hepatic + GI.Bleed + 
##     Tumor + Immunosupperssion + Transfer.hx + MI + age + sex + 
##     edu + DASIndex + APACHE.score + Glasgow.Coma.Score + blood.pressure + 
##     WBC + Heart.rate + Respiratory.rate + Temperature + PaO2vs.FIO2 + 
##     Albumin + Hematocrit + Bilirubin + Creatinine + Sodium + 
##     Potassium + PaCo2 + PH + Weight + DNR.status + Medical.insurance + 
##     Respiratory.Diag + Cardiovascular.Diag + Neurological.Diag + 
##     Gastrointestinal.Diag + Renal.Diag + Metabolic.Diag + Hematologic.Diag + 
##     Sepsis.Diag + Trauma.Diag + Orthopedic.Diag + race + income + 
##     RHC.use

require(rpart)
cart.fit <- rpart(out.formula2, data = ObsData)

6.3.4.2.1 CART Variable importance

cart.fit$variable.importance

##            DASIndex              Cancer               Tumor                 age 
##         123.2102455          33.4559400          32.5418433          24.0804860 
##   Medical.insurance                 WBC                 edu Cardiovascular.Diag 
##          14.5199953           5.6673997           3.7441554           3.6449371 
##          Heart.rate      Cardiovascular         Trauma.Diag               PaCo2 
##           3.4059248           3.1669125           0.5953098           0.2420672 
##           Potassium              Sodium             Albumin 
##           0.2420672           0.2420672           0.1984366

6.3.4.2.2 AUC

require(pROC)
obs.y2<-ObsData$Death
pred.y2 <- as.numeric(predict(cart.fit, type = "prob")[, 2])
rocobj <- roc(obs.y2, pred.y2)

## Setting levels: control = No, case = Yes

## Setting direction: controls < cases

rocobj

## 
## Call:
## roc.default(response = obs.y2, predictor = pred.y2)
## 
## Data: pred.y2 in 2013 controls (obs.y2 No) < 3722 cases (obs.y2 Yes).
## Area under the curve: 0.5981

plot(rocobj)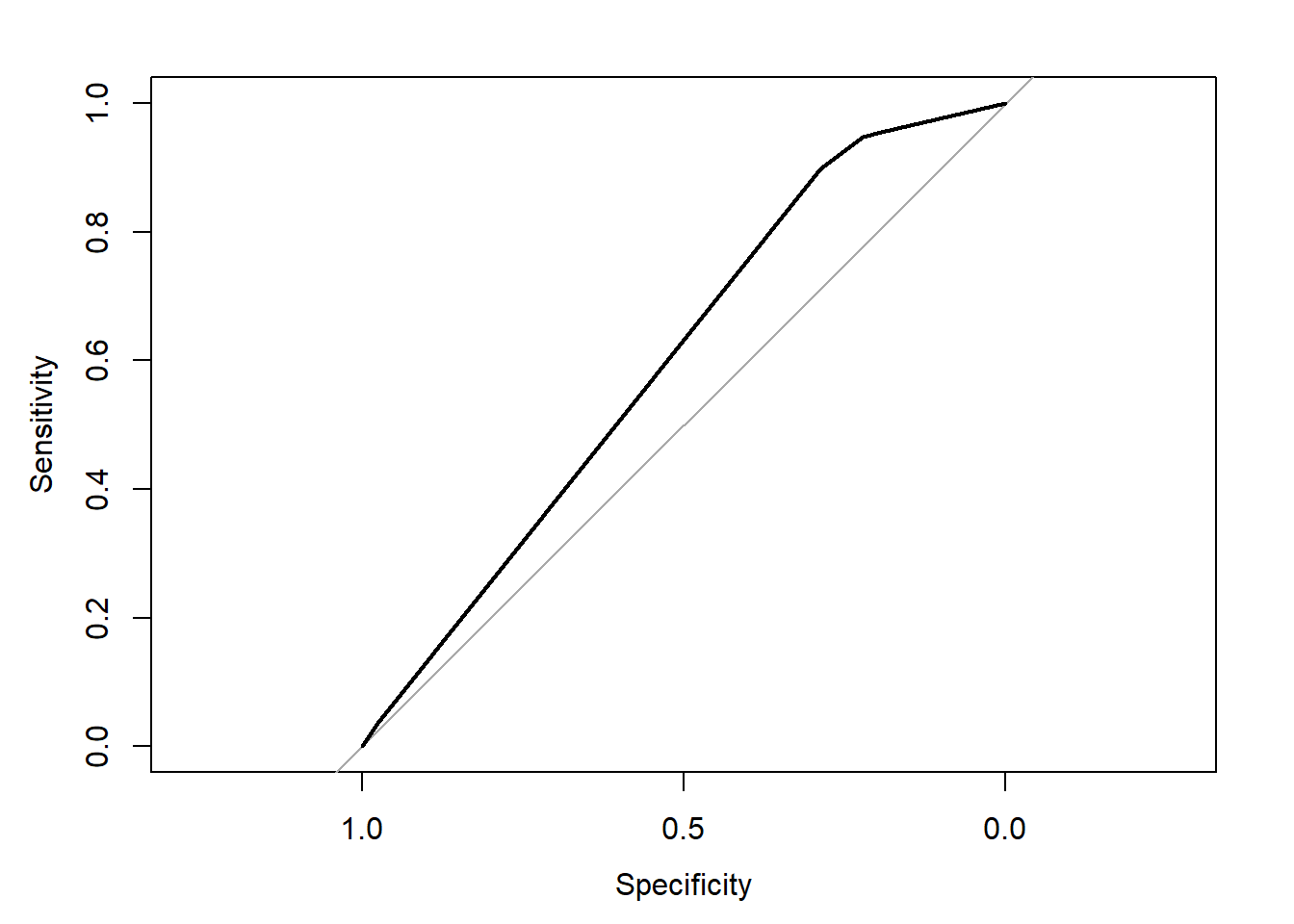

auc(rocobj)

## Area under the curve: 0.5981

6.3.4.3 Cross-validation CART

set.seed(504)
require(caret)
ctrl<-trainControl(method = "cv", number = 5, 
                   classProbs = TRUE,
                   summaryFunction = twoClassSummary)
# fit the model with formula = out.formula2
fit.cv.bin<-train(out.formula2, trControl = ctrl,
               data = ObsData, method = "rpart",
              metric="ROC")
fit.cv.bin

## CART 
## 
## 5735 samples
##   50 predictor
##    2 classes: 'No', 'Yes' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 4587, 4589, 4587, 4589, 4588 
## Resampling results across tuning parameters:
## 
##   cp           ROC        Sens       Spec     
##   0.007203179  0.6304911  0.2816488  0.9086574
##   0.039741679  0.5725283  0.2488649  0.8981807
##   0.057128664  0.5380544  0.1287804  0.9473284
## 
## ROC was used to select the optimal model using the largest value.
## The final value used for the model was cp = 0.007203179.

# extract results from each test data 
summary.res <- fit.cv.bin$resample
summary.res

##         ROC      Sens      Spec Resample
## 1 0.6847220 0.3746898 0.8590604    Fold1
## 2 0.6729625 0.2985075 0.8924731    Fold2
## 3 0.6076153 0.2754342 0.9287634    Fold5
## 4 0.5873154 0.2238806 0.9274194    Fold4
## 5 0.5998401 0.2357320 0.9355705    Fold3

6.4 Ensemble methods (Type I)

Training same model to different samples (of the same data)

6.4.1 Cross-validation bagging

Bagging or bootstrap aggregation
- independent bootstrap samples (sampling with replacement, B times),
- applies CART on each i (no prunning)
- Average the resulting predictions
- Reduces variance as a result of using bootstrap

set.seed(504)
require(caret)
ctrl<-trainControl(method = "cv", number = 5,
                   classProbs = TRUE,
                   summaryFunction = twoClassSummary)
# fit the model with formula = out.formula2
fit.cv.bin<-train(out.formula2, trControl = ctrl,
               data = ObsData, method = "bag",
               bagControl = bagControl(fit = ldaBag$fit, 
                                       predict = ldaBag$pred, 
                                       aggregate = ldaBag$aggregate),
               metric="ROC")

## Warning: executing %dopar% sequentially: no parallel backend registered

fit.cv.bin

## Bagged Model 
## 
## 5735 samples
##   50 predictor
##    2 classes: 'No', 'Yes' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 4587, 4589, 4587, 4589, 4588 
## Resampling results:
## 
##   ROC        Sens       Spec     
##   0.7506666  0.4485809  0.8602811
## 
## Tuning parameter 'vars' was held constant at a value of 63

bagging improves prediction accuracy
- over prediction using a single tree
Looses interpretability
- as this is an average of many diagrams now
But we can get a summary of the importance of each variable

6.4.1.1 Bagging Variable importance

caret::varImp(fit.cv.bin, scale = FALSE)

## ROC curve variable importance
## 
##   only 20 most important variables shown (out of 50)
## 
##                    Importance
## age                    0.6159
## APACHE.score           0.6140
## DASIndex               0.5962
## Cancer                 0.5878
## Creatinine             0.5835
## Tumor                  0.5807
## blood.pressure         0.5697
## Glasgow.Coma.Score     0.5656
## Disease.category       0.5641
## Temperature            0.5584
## DNR.status             0.5572
## Hematocrit             0.5525
## Weight                 0.5424
## Bilirubin              0.5397
## income                 0.5319
## Immunosupperssion      0.5278
## RHC.use                0.5263
## Dementia               0.5252
## Congestive.HF          0.5250
## Hematologic.Diag       0.5250

6.4.2 Cross-validation boosting

Boosting
- sequentially updated/weighted bootstrap based on previous learning

set.seed(504)
require(caret)
ctrl<-trainControl(method = "cv", number = 5,
                   classProbs = TRUE,
                   summaryFunction = twoClassSummary)
# fit the model with formula = out.formula2
fit.cv.bin<-train(out.formula2, trControl = ctrl,
               data = ObsData, method = "gbm",
               verbose = FALSE,
               metric="ROC")
fit.cv.bin

## Stochastic Gradient Boosting 
## 
## 5735 samples
##   50 predictor
##    2 classes: 'No', 'Yes' 
## 
## No pre-processing
## Resampling: Cross-Validated (5 fold) 
## Summary of sample sizes: 4587, 4589, 4587, 4589, 4588 
## Resampling results across tuning parameters:
## 
##   interaction.depth  n.trees  ROC        Sens       Spec     
##   1                   50      0.7218938  0.2145970  0.9505647
##   1                  100      0.7410292  0.2980581  0.9234228
##   1                  150      0.7483014  0.3487142  0.9030028
##   2                   50      0.7414513  0.2960631  0.9263816
##   2                  100      0.7534264  0.3869684  0.8917212
##   2                  150      0.7575826  0.4187512  0.8777477
##   3                   50      0.7496078  0.3626125  0.9070358
##   3                  100      0.7579645  0.4078244  0.8764076
##   3                  150      0.7637074  0.4445909  0.8702298
## 
## Tuning parameter 'shrinkage' was held constant at a value of 0.1
## 
## Tuning parameter 'n.minobsinnode' was held constant at a value of 10
## ROC was used to select the optimal model using the largest value.
## The final values used for the model were n.trees = 150, interaction.depth =
##  3, shrinkage = 0.1 and n.minobsinnode = 10.

plot(fit.cv.bin)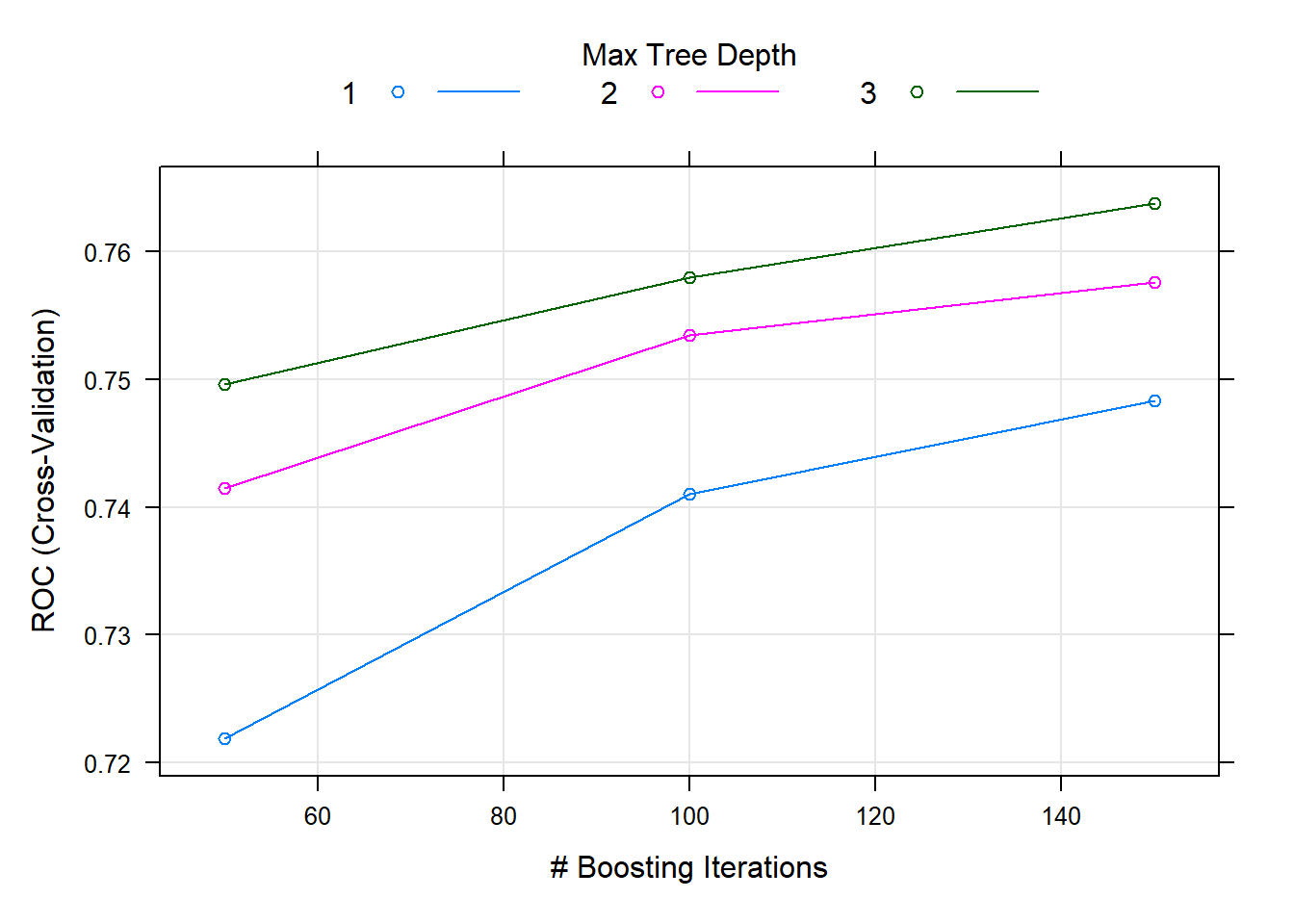

6.5 Ensemble methods (Type II)

Training different models on the same data

6.5.1 Super Learner

Large number of candidate learners (CL) with different strengths
- Parametric (logistic)
- Non-parametric (CART)
Cross-validation: CL applied on training data, prediction made on test data
Final prediction uses a weighted version of all predictions
- Weights = coef of Observed outcome ~ prediction from each CL

6.5.2 Steps

Refer to this tutorial for steps and examples!