20  Deep Learning

Recent work extends traditional hdPS analyses by introducing and explaining neural representation learning methods for causal inference in observational studies. It focuses on NHANES data (2013–2018) and highlights how recent innovations in machine learning can address residual confounding and model misspecification challenges commonly encountered in high-dimensional data settings.

Based on recent work by Karim & Wang (2025).

20.1 Plasmode Simulation

Simulation Element	Description
Source Dataset	NHANES 2013–2018
Simulation Framework	Plasmode simulation preserving empirical covariate and exposure distributions
Simulated Sample Size	3,000 participants per iteration
Iterations	500 replicates
Prevalence Scenarios	1. Frequent exposure & frequent outcome 2. Rare exposure & frequent outcome 3. Frequent exposure & rare outcome
True Effect	OR = 1 (null); RD = 0
Outcome Generation	Logistic regression model with: - Nonlinear transformations (log, poly) - Interactions - Proxy-derived comorbidity index
Confounding Simulation	Unmeasured confounding mimicked using high-dimensional proxy variables

20.2 Estimators Compared

Method	Core Idea	Key Features	Use of Propensity Score	Optimization & Regularization
PSW (hdPS)	Baseline method using logistic regression on investigator and proxy covariates	High-dimensional covariates selected via hdPS	Explicitly modeled via logistic regression	None
TMLE (SL Smooth) (Balzer and Westling 2021)	Semiparametric estimator using Super Learner	Combines outcome and treatment models; uses smooth learners (logistic regression, LASSO, MARS)	Explicitly modeled and used for targeting	Super Learner; Donsker-compliant learners
TMLE (SL Unsmooth)	More flexible TMLE with XGBoost in Super Learner	Allows complex nonlinearities; lower variance reliability in small samples	Explicitly modeled and used for targeting	Super Learner including unsmooth learners (e.g., XGBoost)
DCTMLE (Zivich and Breskin 2021)	TMLE with double cross-fitting	Reduces overfitting in TMLE with flexible learners	Explicitly modeled and used for targeting	Double cross-fitting for robustness
TARNET (Shalit, Johansson, and Sontag 2017)	Neural net with treatment-agnostic shared representation	Two heads for outcome under treatment/control; most precise in frequent exposure/outcome	Not used explicitly	Targeted regularization; Adam + SGD with early stopping
Dragonnet (Shi, Blei, and Veitch 2019)	Neural net that jointly models outcomes and propensity score	Adds third head for PS; enforces balance and semiparametric alignment	Modeled as an explicit third output	Targeted regularization; multitask learning
NEDnet (Shi, Blei, and Veitch 2019)	Sequential neural network for treatment then outcome	Stage 1: predict treatment; Stage 2: freeze representation and predict outcomes	Modeled separately in Stage 1	Targeted regularization; two-stage optimization

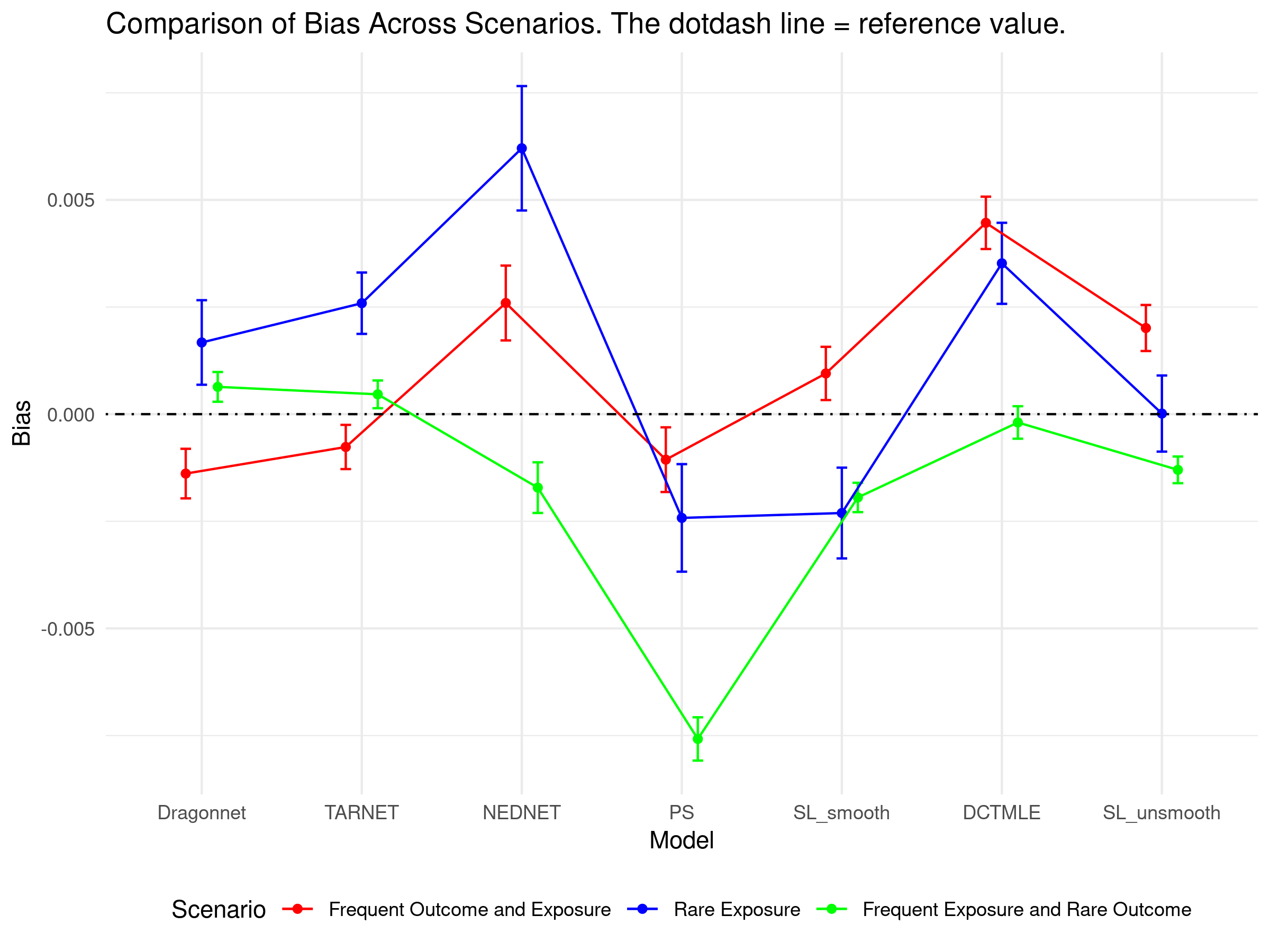
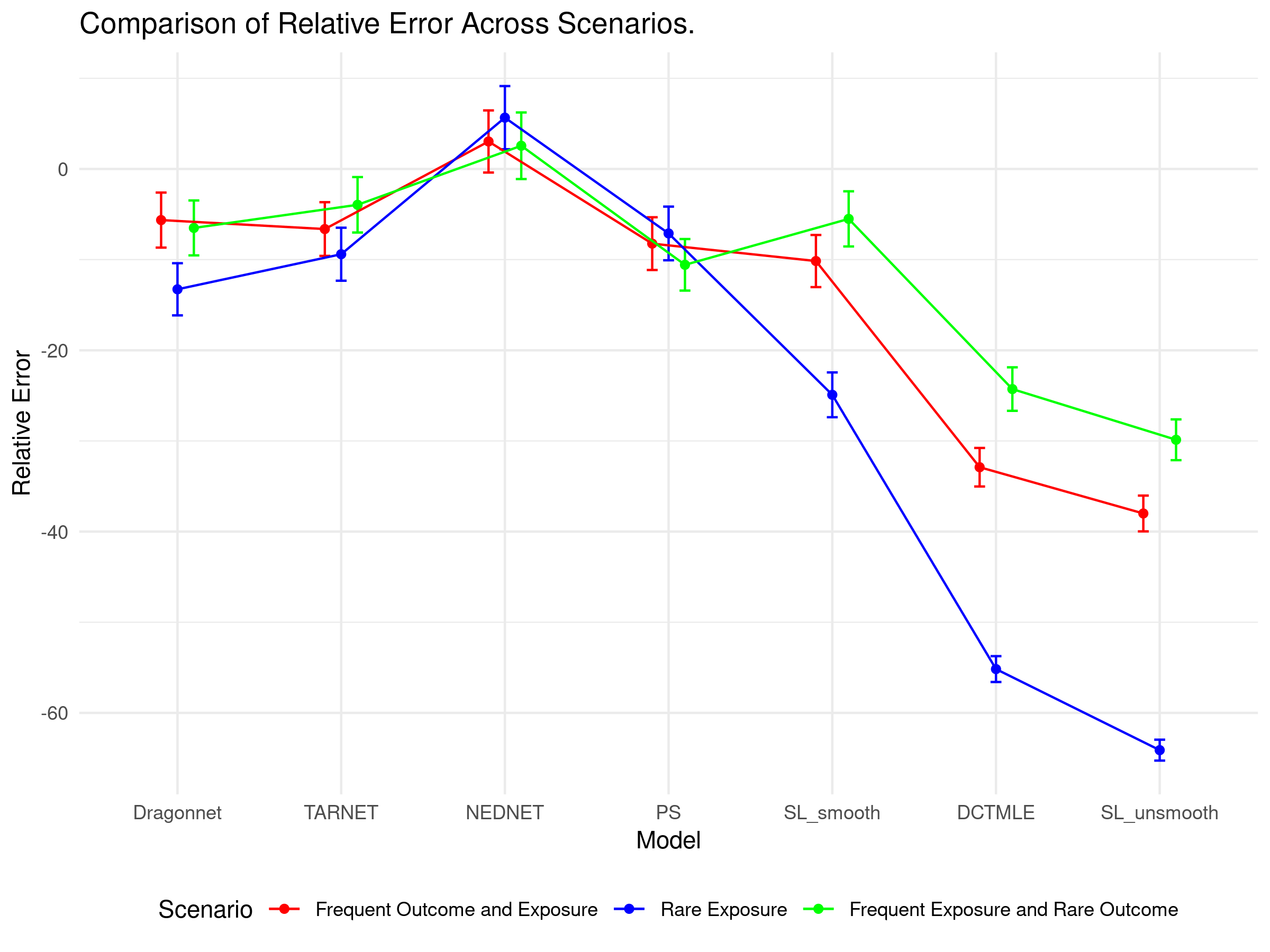
20.3 Simulation Results

Figure 1. Bias across Methods in NHANES Plasmode Simulation

Figure 2. Relative error across Methods in NHANES Plasmode Simulation

Results are fully accessible via a Shiny app:

👉 Interactive Causal Benchmark App

Explore bias, SEs, and coverage metrics across methods and simulation conditions.

20.4 Conclusion

• PSW remains an interpretable benchmark
• TMLE and neural methods extend this framework by improving bias-variance trade-offs and enabling better performance in complex settings
• Among deep learning methods, Dragonnet offers the best average trade-off; NEDnet excels in coverage but is computationally heavy; TARNET offers precision
• These methods are particularly useful when dealing with residual confounding, nonlinear effects, and proxy variable structures

Balzer, Laura B, and Ted Westling. 2021. “Demystifying Statistical Inference When Using Machine Learning in Causal Research.” American Journal of Epidemiology.

Shalit, Uri, Fredrik D Johansson, and David Sontag. 2017. “Estimating Individual Treatment Effect: Generalization Bounds and Algorithms.” In International Conference on Machine Learning, 3076–85. PMLR.

Shi, Claudia, David Blei, and Victor Veitch. 2019. “Adapting Neural Networks for the Estimation of Treatment Effects.” Advances in Neural Information Processing Systems 32.

Zivich, Paul N, and Alexander Breskin. 2021. “Machine Learning for Causal Inference: On the Use of Cross-Fit Estimators.” Epidemiology (Cambridge, Mass.) 32 (3): 393.